Abstract
논문에서는 complex high-dimensional densities를 모델링 하는 NICE를 소개합니다.
주어진 데이터들에 대해서, 적당한 latent space로 보내는 non-linear deterministic tarnsformation을 학습합니다.
이러한 transformation을 jacobian의 행렬식 그리고 jacobian의 역이 유일하게 하면서 complex non-linear transformation을 갖도록 구성합니다.
training criterion은 exact log-likelihood이므로 굉장히 tractable 한 것이 장점입니다.
Introduction
Good representation이란 뭘까요? 바로 data에 대한 distribution이 모델링 하기 쉬운 것을 의미한다고 합니다.
이 논문에서는 data를 새로운 space로 보내는 \(h = f(x)\)를 학습하여 prior distribution을 보내는 방법을 제시합니다. 이 때 prior distribution은 각 dimension이 독립이라고 가정하여 factorize 할 수 있는 형태 입니다. 그래서 아래처럼 적을 수 있습니다.
$$ p_H(h) = \prod_d P_{H_d}(h_d) $$
근데 생각해보면 우리는 data space -> new space 로 옮기는 형태라서 space를 옮겨줄 때 단순히 변수만 치환해주는 것이 아니라 치환했을 때 space의 단위 또한 달라지기 때문에, 이로 인해 발생하는 변화도 고려해줘야 합니다.
Notation : new pdf, data pdf -> \(p_H, p_X\)
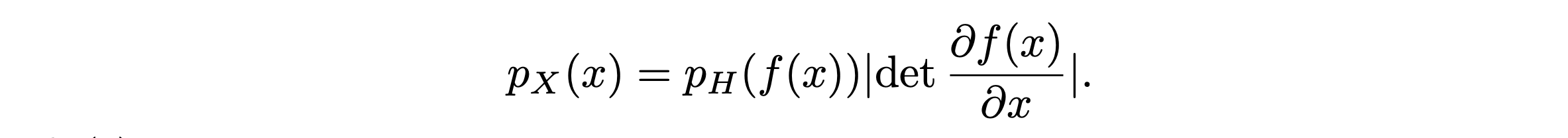
\(h = f(x)\) 를 통해 좌항을 우항처럼 바꿔줄 수 있습니다. 근데 변수를 바꾸면서 일어나는 space의 변화를 우항에서 Jacobian determinant의 절댓값을 곱해주고 있습니다.
이는 수식적으로 pdf를 전 구간에서 적분 했을 때 1이 되는 것을 이용하여 \(p_X(x)\)와 \(p_H(h)\)의 전 구간 적분을 같다고 놓은 후 미분을 통해 식을 유도하면 자연스럽게 나옵니다. 이에 대한 부분은 flow based 자체를 다루는 다른 블로그 포스트에 잘 나와있으니 봐보시는걸 추천드립니다.
위의 식에 나와있듯이 어떤 tranformation을 적용해서 변수를 치환해주기 위해서는 jacobian의 determinant를 구해야합니다. 그렇기 때문에 이 논문에선 함수 f를 jacobian의 행렬식을 구하기 쉽도록 구성했습니다.
그리고 또 중요한 것은 inverse 또한 간단해야한다는 것 입니다. 위의 data를 latent space로 보내는 transformation을 훈련 한 다음 이의 역을 적용해서 latent space에서 하나의 latent를 뽑아와서 data 또한 만들어 내는 것도 가능합니다. 이게 궁극적인 목표이기도 하구요.
그렇기 때문에 이 transformation의 inverse를 취하는 것 또한 쉬워야합니다.
위를 만족시켜줄 수 있도록 input \(x\)를 split 하여 \(x_1, x_2\)로 나누고 이 각각에 대해 다르게 transformation을 적용합니다.
$$ y_1 = x_1 $$
$$ y_2 = x_2 + m(x_1) $$
이 때 m은 어떤 complex function 입니다. (MLP) 이 식에서 jacobian의 determinant는 무조건 1이고, inverse 또한 유일하게 존재합니다.
inverse는 아래와 같습니다.
$$ x_1 = y_1 $$
$$ x_2 = y_2 - m(y_1) $$
Learning Bijective Transformation of Continuous Probabilities
위의 글에서 갑자기 pdf 가 나와서 논리의 비약이 생겼을 수도 있습니다.
이전 VAE글에서도 설명 했듯이 loglikelihood based GM에서 저희의 목적은 \(\log p(x)\)를 최대화 하는 것입니다.
\(p_X(x)\)를 real data에 대한 pdf 이라 생각했을 때 저희의 목적은 \(\log p_X(x)\)를 최대화 하는게 됩니다.
앞에서 pdf 에 대해 change of variable을 적용 할 때 뒤에 jacobian determinant가 붙는 것을 봤습니다. 이를 통해 \(log p_X(x)\)에 대한 식을 다시 써봅시다.

그럼 이처럼 식이 나오게 됩니다. space를 옮겼을 때 \(p_H(h)\)를 factorize 형태의 distribution이라고 칭했기 때문에, log에 sum으로 표현할 수 있습니다.

좀 직관적으로 말하자면 x는 data들이고, f 는 MLP 라고 생각하시면 됩니다. MLP의 output에 대해 space의 domain을 바꿔주기 위해 jacobian det가 붙습니다.
여기에서 \(p_H\)를 우리가 접근을 쉽게할 수 있는 (Log probability를 쉽게 뽑아낼 수 있는) gaussian distribution이나 logistic distribution으로 잡아둬서 \(\log p_X(x)\)를 구하기 쉽게 한 다음 이 log likelihood를 최대화 하는 방향으로 학습하게 된다면, 궁극적으로 저희의 목적에 맞는 Log likelihood를 높여줄 수 있습니다. 이렇게 훈련을 하게 된다면 \(f(.)\)는 주어진 data를 저희가 의도한 간단한 distribution으로 잘 보낼 수 있습니다.
접근이 쉬운 distribution에서 latent를 뽑아온 다음, 이 f에 역을 취해줘서 latent를 넣어주면 실제 이미지 또한 얻어올 수 있습니다.
이게 flow based GM 의 방법입니다.
Architecture
Triangular Structure
앞에서 말한 조건들 중 determinants를 구하기 쉬운 조건은 뭘까요??
Triangular matrices인 경우 deteminants를 구하기 쉽습니다. 이 뿐만아니라 역을 취하는 것 또한 매우 쉽기 때문에, 논문에서는 jacobian이 triangular matrix가 될 수 있도록 구성하게 됩니다.
이걸 만족하는 구조로서 Coupling Layer를 사용하게 됩니다.
Coupling Layer

General Coupling Layer

일반적인 Coupling Layer의 형태입니다. 위 Fig에도 나와 있듯이 저런 흐름으로 진행이 됩니다.
근데 저희가 앞에서 말했듯이 이 흐름의 역에 해당하는 것을 통해 샘플링을 진행하게 됩니다. 그래서 단순히 g를 더하기로 정의해서 역일 때는 빼줍니다.

이런 형태의 coupling layer의 jacobian matrix를 구해보면 triangular matrix로 나옵니다.

그래서 위 자코비안을 살펴보면 우측 하단에 해당하는 미분만 구해주면 된다는 것을 알 수 있습니다. (쉬움.)
하지만 우측 하단 또한 1로 나옵니다. 더하기로 단순 진행했기 때문!
그럼 log에 대한 jacobian의 determinant는 0이 나오기 때문에 무시해도 됩니다. 이처럼 coupling layer를 여러개 쌓더라도 신경 쓰지 않아도 됩니다.
Allowing Rescaling
근데 이렇게 space의 volume을 유지하게 되는게 이슈로서 남을 수 있습니다.
이를 위해 f : x -> z 의 마지막 레이어에 Scaling 요소를 넣어줍니다. 이때 스케일링은 diagonal factor로 곱해줍니다.
이런 scaling을 적용해준다면 space의 Volume도 변하기 때문에 Jacobian의 determinant는 unit이 아니게 됩니다.
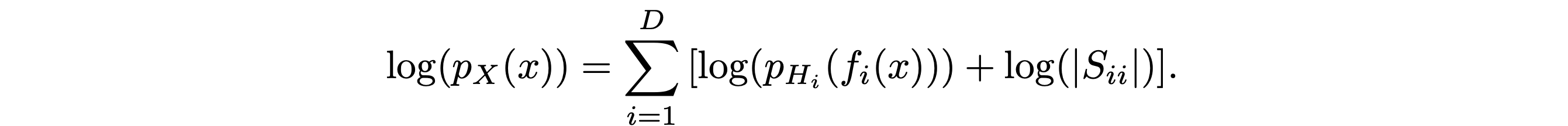
논문에서 실험 중 PCA로 분석해본 결과 diag \(S_{ii}\)에 큰 scale값이 있다면 해당 dimension을 덜 중요하게 여기는 방향으로 훈련이 됩니다.
'Generative Model' 카테고리의 다른 글
| Glow : Generative Flow with Invertible 1 x 1 Convolutions (0) | 2021.10.03 |
|---|---|
| Density Estimation Using Real NVP (0) | 2021.09.26 |
| PixelCNN의 실행 흐름 (0) | 2021.09.22 |
| Generating Diverse High-Fidelity Images with VQ-VAE2 (0) | 2021.09.20 |
| Neural Discrete Representation Learning : VQ-VAE (0) | 2021.09.17 |


