저번 포스팅했던 NICE에 이어 Real NVP에 대한 설명을 하고자 합니다.
Real NVP란 real-valued non-volume preserving transformation을 사용했단 뜻인데, NICE에서는 transformation을 적용할 때 단순 더하기로 진행했기 때문에 volume을 보존하는 성질을 지녔습니다. 이런 이슈때문에 x->z 로 가는 방향 기준 마지막에 scaling layer를 구성했습니다.
이 논문에서는 단순 더하기가 아닌 volume을 보존하지 않는 transformation을 차용했습니다.
아이디어 자체는 어렵지 않아서 구현도 그저 어렵지 않겠지라 생각했는데, 구현이 어렵더군요. 여기저기 구현된 것을 찾아보니 클래스에 대한 재귀호출로 쉽게 풀어냈긴 했더라구요. 저는 반복문으로 짰습니다. 그러니 좀 어렵더라구요 헷갈리고..
Introdution
앞에서 말했듯이 NICE는 volume preserving transformation (addition) 을 사용했습니다.
하지만 저희가 관심있는 데이터들은 고차원으로 구성되는 경우가 많습니다. 이는 모델을 세울 때 complexity를 충분히 파악할 수 있게끔 세워야함을 의미합니다.
하지만 NICE는 volume preserving transformation으로 우리가 원하는 직관적이고 간단한 latent space로 보내게 됩니다. 이로인해 충분히 complexity를 파악하지 못하는 것이죠.
대신 이 논문에선 non-volume preserving transformation을 적용하는 모델을 제안합니다.
Model Definition
Key : 좀 더 flexible한 아키텍쳐, 강력한 bijective functions 제안.
이전 포스트 NICE에서 언급했었던 Change of Variable 에 대한 수식은 적어놓기만 하고 다른 이야기를 하겠습니다.


위에서 설명했던 고차원의 데이터를 우리가 원하는 직관적이고 간단한 latent space로 보내는 과정에 대한 Fig가 나와있습니다.
위 Figure가 굉장히 잘 나타내어 주고 있는데요, data space는 어떤 manifold를 형성하는 고차원 데이터 공간이고 우리는 이것을 직관적이고 간단한 고차원 latent space로 보내줄 것 입니다. 간단한 고차원 latent space란 NICE에서도 언급했듯이 dimension들이 서로 독립인 직관적인 latent distribution입니다. (Gaussian disribution, Logistic distribution...)
Inference 단계에선 x를 z로 보내줄거고, Generation 단계에선 z를 x로 보내줍니다.
Inference(train)의 함수를 기반으로 한 역함수를 통해 z를 x로 보내줄 것이기 때문에 bijective 해야합니다. NICE에서 언급했듯이, Jacobian Matrix는 Triangular matrix여야 하구요.
이런 성질을 잘 가지고 있도록 구조를 짜야합니다.
Coupling Layer

NICE 때 처럼 Coupling Layer 형태의 레이어를 통해 역함수를 구하기 쉬우며, Jacobian이 triangular matrix 형태를 띄도록 했습니다.
특이한 점이 있다면 scale factor s를 통해서 volume을 유지하지 않도록 했습니다.

식은 이렇구요. scale factor에 exp가 붙었는데 이는 jacobian의 determinant를 구할 때 log를 상쇄시켜주기 위함입니다.
그리고 s와 t라는 factor는 complex network (ResNet)을 통해 구하게 됩니다.
Properties
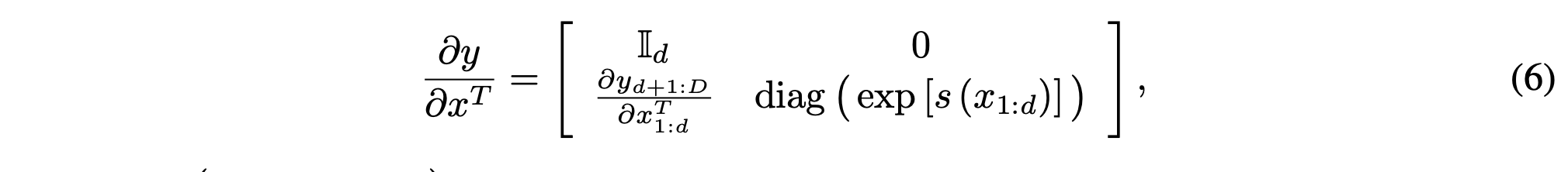
NICE 때와 동일하게 Coupling Layer 형식을 차용했기 때문에 Jacobian Matrix 또한 Lower Triangular Matrix 형태를 띄게 됩니다.
그렇다면 Log Likelihood를 구할 때 사용되는 jacobian determinant는 log scale들의 합이 되겠죠? 구하기 아주 쉽습니다.
그리고 역을 취하는 것 또한 매우 쉽습니다. 이것도 NICE와 굉장히 유사합니다.
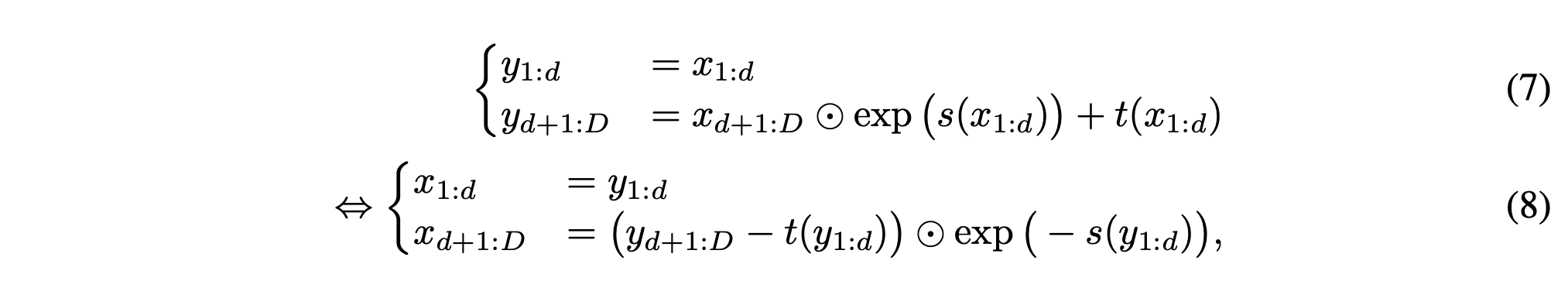
scale과 translation에 대한 역을 취하면 아래처럼 됩니다. 굉장히 간단합니다.
Masked Convolution
근데 저희가 말했듯이 ResNet을 통해 더 복잡한 complexity를 capture 하고자 했습니다. (feature)
NICE 때와는 다르게 Flatten 된 형태가 아니라 Image 형태의 feature map에 대해 mask를 적용해야합니다. (동일한 마스크 적용 시 연산에 참여를 안하는 데이터가 존재 할 수도 있기 때문.)
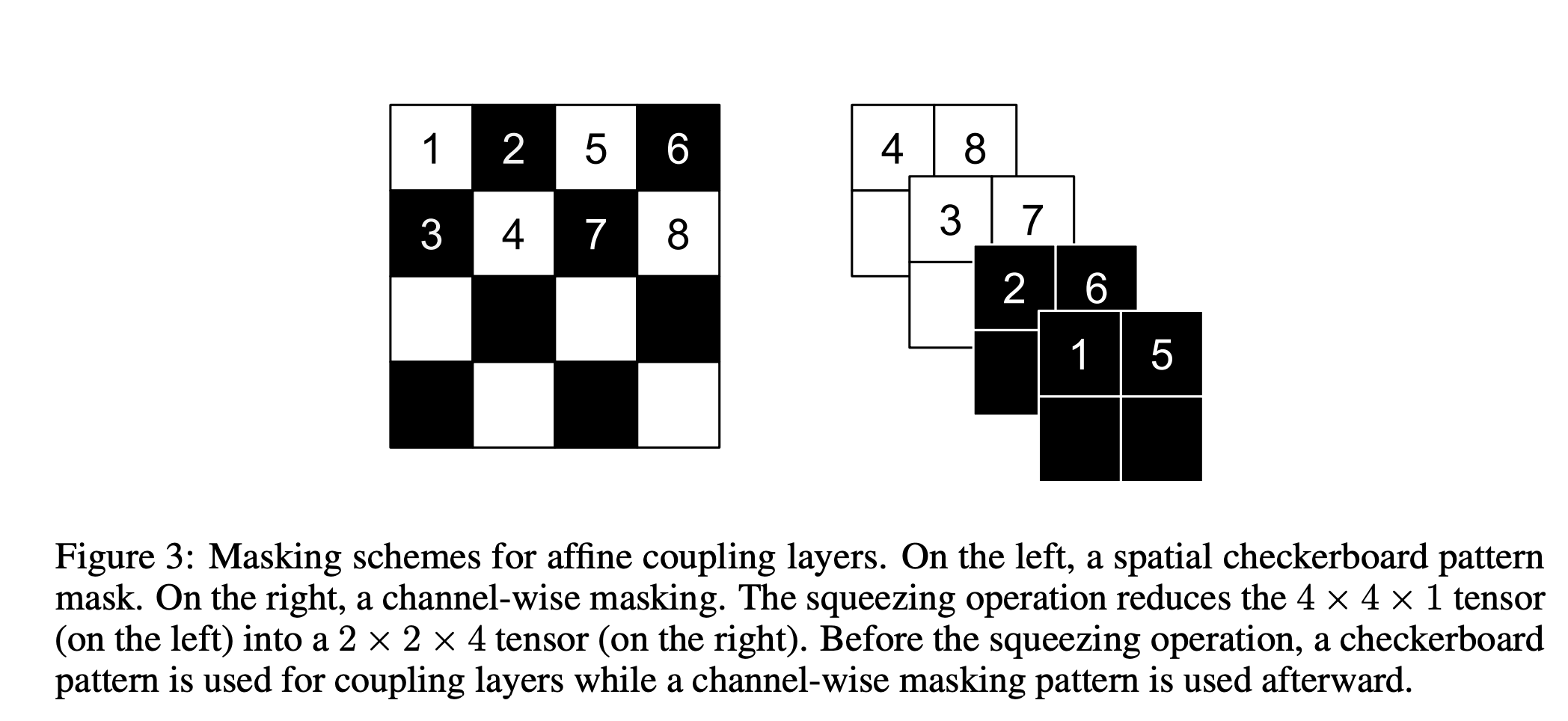
그래서 논문에선 Spatial(H, W) 부분과 Channel(C) 두가지 종류의 마스크로 나눠서 제안합니다.
Figure 3를 보시면, 대략 어떻게 구현되는지 알 수 있습니다.
Checkerboard 형식의 경우에는 위치적 특성에 대해 (H,W)에서 마스킹을 취해주고, Channel wise 형식의 경우에는 채널에 대해 마스킹을 취해줍니다. (NICE의 Flatten에서 했던 것처럼)
Multi-scale architecture
이제 각 한층의 형식을 봤으니 Multi scale을 고려할 수 있는 아키텍쳐를 생각해봅시다.
알다시피 이 flow based model을 구성하는 transformation들은 가역이어야 합니다. 그렇기 때문에 어떤 트릭 없이 그저 층을 쌓는다면 동일한 shape에 대해서만 생각할 수 밖에 없습니다.
하지만 Multi-scale에 대해 고려해줄 수 있게 논문에선 Squeezing 이라는 개념을 도입합니다.
squeezing operation이란 \(s \times s \times c\) 형태의 텐서를 \({s \above 1pt 2} \times {s \above 1pt 2} \times 4c\) 로 바꿔주는 것 입니다.
이 방법으로 shape을 변환할 수 있고, 이의 inverse operation 또한 간단합니다.
Fig.3의 우측 그림은 이를 잘 나타내줍니다.
그리고 제가 구현하기 전에 간과하고 있던 부분이 있었는데, 바로 아키텍쳐 구성의 진행방향입니다.
우선 처음엔 3개의 coupling layer (spatial checkerboard masking) -> Squeezing -> (3 x coupling layer(channelwise masking)) -> Unsqueezing.. 이런식으로 쌓아갑니다.
하지만 여기에서 주의해야 할 점은 위 coupling - squeezing - coupling - Unsqueezing 과정이 끝나고 이에 대한 output에 Squeezing을 취해준 후 절반으로 나눕니다.
이 후 절반만 가져와서 또 coupling - squeezing - coupling 블럭에 넣어줍니다. 이 과정을 반복하면 절반씩 줄어져가는 x의 나머지들이 존재하게 됩니다.
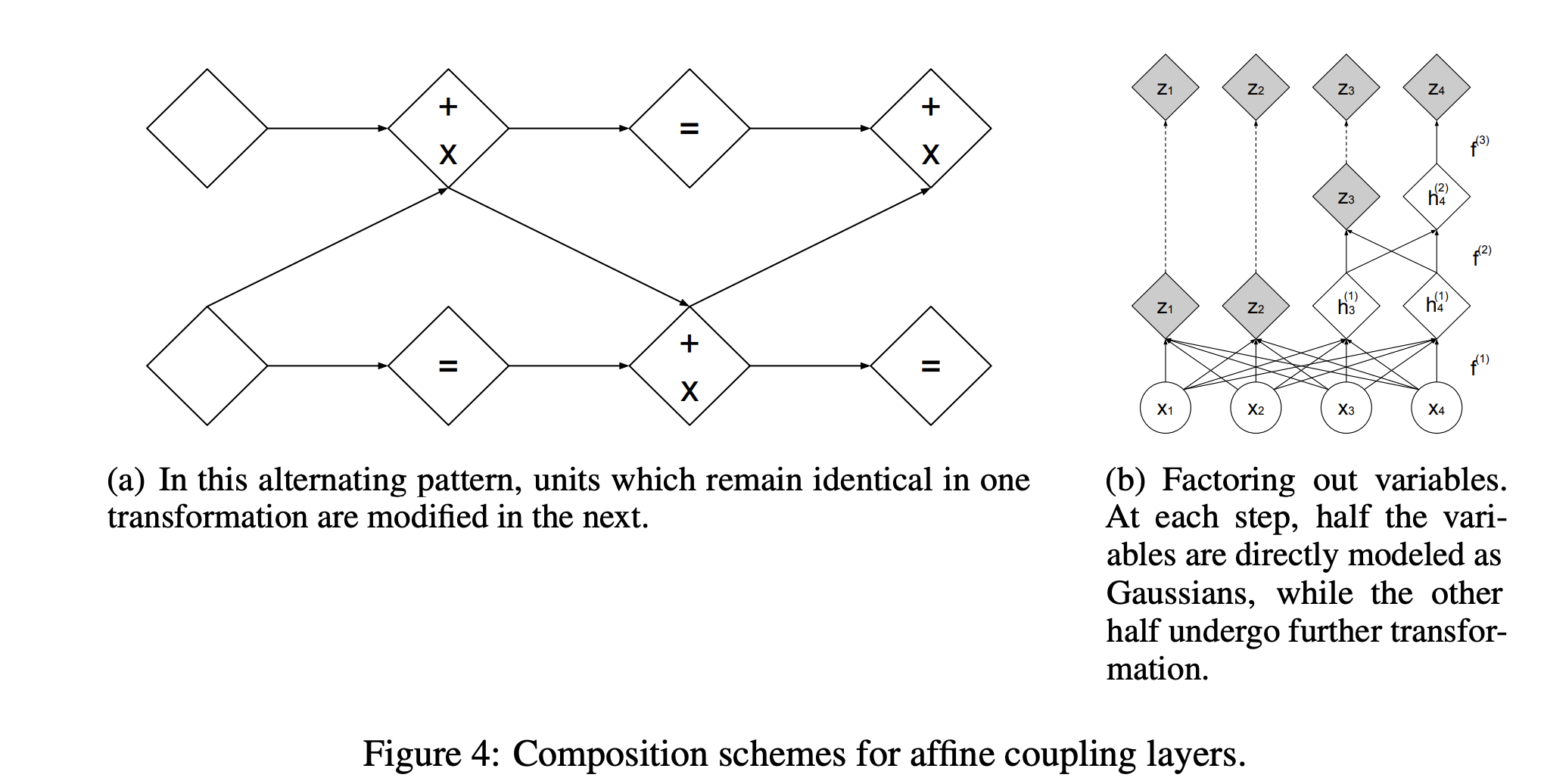
이 때 이 x 나머지들을 모아놓은 것들과 마지막 output x를 차례대로 concat 해나가면 되는데, 중간중간 squeezing 과정이 들어있기 때문에 Unsqueezing도 중간중간 넣어줘야합니다.
위처럼 구현하게 되면 Fig 4의 (b) 흐름과 동일해집니다.
Batch Normalization
이 구조에서 s, t factor에 대해 batch normalization과 Weight normalization을 적용했습니다.
이 뿐만 아니라 Coupling layer의 output에도 Batch normalization을 적용했습니다.
그럼 이에 따른 Jacobian determinant가 나오게 됩니다.
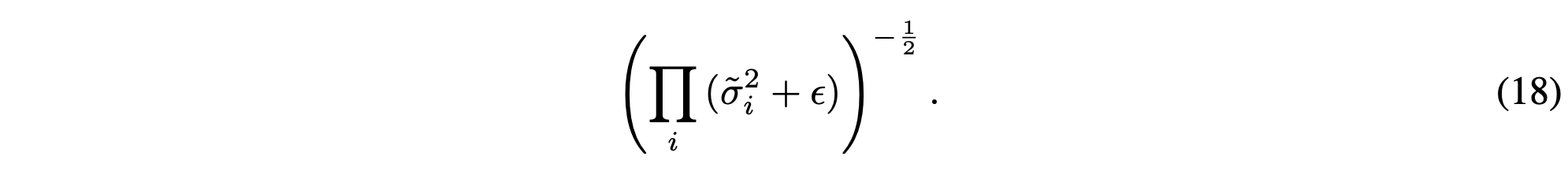
Batch Normalization은 위와 같은 형태의 아주 간단한 Jacobian determinant 를 내놓게 됩니다. (rescaling factor)
Batch Normalization의 적용과 Determinant의 적용으로 인해 더 깊은 Coupling layer를 쌓을 수 있게 하였고 불안정성 문제를 감소시켰다고 합니다.
'Generative Model' 카테고리의 다른 글
| Flow++ : Improving Flow-Based Generative Models with Variational Dequantization and Architecture Design (0) | 2021.10.10 |
|---|---|
| Glow : Generative Flow with Invertible 1 x 1 Convolutions (0) | 2021.10.03 |
| NICE : Non-linear Independent Components Estimation (0) | 2021.09.24 |
| PixelCNN의 실행 흐름 (0) | 2021.09.22 |
| Generating Diverse High-Fidelity Images with VQ-VAE2 (0) | 2021.09.20 |


