
저번 포스트에서는 전체적인 상황, 그리고 이를 위한 solution에 대해서 알아보고 Reparameterization에 대한 이유에 대해서도 알아보았습니다. (AEVB)
이번에는 논문에서 제시된 Example : Variational Auto-Encoder에 대해 알아보겠습니다.
Example : Variational Auto-Encoder
사견
autoencoder 형식이다.
간단하게 말하면 sample x를 통해 mean과 var를 만들고 이 정보를 통해 latent z 를 샘플링 한 후 다시 x를 만들어낸다.
여기에서 주목해야할 점은 "무작위성"이다.
x -> z로 보낸다. 하지만 여기에서의 z는 어느정도의 무작위성을 갖는다. mean + std * normal 형태로 만들어지니까..
자연스럽게 data distribution에 대응되는 latent space같이 피팅된다.
이 논문에서는 True posterior를 근사하는 recognition model을 \(q_\phi (z|x)\)로 표기하고 이를 probabilistic encoder처럼 사용합니다. 여기에서 x라는 데이터 포인트는 z라는 latent code를 통해서 생성되는데 이때 z라는 latent codes는 어떤 distribution을 이룹니다. (예를 들면 가우시안)
위 encoder와 비슷한 측면으로, \(p_\theta(x|z)\)라는 probabilistic decoder도 존재합니다.
Auto Encoder의 구조를 사용해서 \(q_\phi (z|x)\)로 true postrior \(p_\theta(z|x)\)를 근사할 수 있게하였습니다. (Variational Inference) x가 주어지고 z가 나오도록.
자 그럼 위에서 언급한 encoder decoder를 모델로 표현을 해봅시다.

우선 \(p_\theta(z)\)라는 z에 대한 prior가 multivariate Gaussian \(N(z;0,I)\)를 따른다고 합시다. 여기에서 z에 대한 prior는 \(\theta\)와 관계없이 고정된 형태입니다.
그리고 decoder에서 z가 MLP를 통해 나온 output의 각 픽셀(이미지의 경우)의 값이 real data냐, 아니면 binary data냐에 따라 p_\theta(x|z)가 multivariate Gaussian을 따르는지 아니면 Bernoulli 를 따른는지가 결정됩니다.
단 생각해야할 점은 true posterior \(p_\theta(z|x)\)가 intractable 하다는 점입니다.
우리는 이 상황에서 이 intractable한 true posterior를 근사하기 위해 \(q_\phi(z|x)\)를 사용하게 됩니다.
이는 approximator는 자유도가 높으면서 true posterior가 적당한 파라미터를 갖는 (diagonal covariance)형태로 가정하게 됩니다.
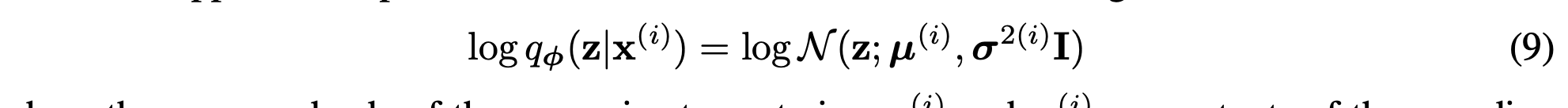
그리고 이전 포스트에서 증명했듯이 reparameterization trick을 사용하게 됩니다.
이전 포스트에서는 likelihood ratio gradient에 의해 높은 Variance를 갖기 때문이라고 했는데, 이 뿐만 아니라 역전파를 진행하기 위해서는 standard normal distribution에서 추출한 \(\epsilon\)을 사용해야합니다. 이는 다른 포스트들에서 잘 설명해주고 있습니다.

자 이제 모델의 구성을 봤으니 Loss로서 사용할 ELBO에 대해 살펴봅시다.
왼쪽 term인 KL Divergence에 대한 요소들에 대해 우리는 다 알고 있습니다. z의 prior를 간단하게 \(N(0,I)\)로 뒀고, \(q_\phi\)는 (9)와 같이 표현되기 때문에 직접적으로 KLD를 계산할 수 있습니다.

이렇게 전체적인 ELBO를 수식적으로 풀어나간다면 위와 같은 식이 나옵니다.
그래서 이에 대해 최적화 하면 됩니다.
보통 앞의 KL Divergence Term이 Regularizer처럼 역할을 수행하고 뒤의 likelihood term이 reconstruction에 해당하는 의미를 지니기 때문에 KL Divergence term을 regularization term, likelihood term을 Reconstruction term이라고 부르기도 합니다.
단 제가 하루종일 VAE만 돌려본 후기로는 reconstruction term을 MSE Loss로 사용하는 것 보다는 BCE Loss로 사용하는게 더 좋은 성능을 보였습니다. (Cifar 10 기준.)
'Generative Model' 카테고리의 다른 글
| Generating Diverse High-Fidelity Images with VQ-VAE2 (0) | 2021.09.20 |
|---|---|
| Neural Discrete Representation Learning : VQ-VAE (0) | 2021.09.17 |
| Variational Auto Encoder를 이해해보자! (3) (0) | 2021.09.14 |
| Variational Auto Encoder를 이해해보자! (1) (0) | 2021.09.12 |
| Denoising Diffusion Probabilistic Model : DDPM (1) | 2021.09.10 |



