Abstract
이 논문에서 제시하는 contributions는 두가지로 볼 수 있는데,
첫번째로는, Variational lower bound의 reparametrization. (standard stochastic gradent method). 이는 차후에 Likelihood-ratio Gradient 와 관련하여 알기 쉽게 수식적으로 풀어나가보도록 하겠습니다.
두번째로는 lower bound estimator 를 통해서 data point당 연속적인 잠재변수를 갖는 i.i.d datasets에서의 posterior를 효과적으로 fitting 가능하다는 것입니다.
보통 알려져있는 VAE는 생성 모델로서 존재하는데, 이와 관련지어 설명하자면 i.i.d datasets의 datapoint 당 연속적인 잠재변수를 갖기 때문에, 잠재변수로 datapoint를 생성할 수 있고 datapoint로부터 잠재변수를 이끌어 낼 수 있음을 뜻합니다.
Introduction
기존에 Intractable posterior에 대해 알아보고자 하는 노력들이 있었는데 (Variational Bayesian), mean field approximation (요소끼리 독립이라서 곱으로 표현하는 방법)을 통해 근사하는 방법은 그 또한 intractable합니다.
논문에서는 SGVB(Stochastic Gradient Variational Bayesian)를 사용해서 효과적으로 연속적인 잠재변수, 파라미터에 대한 posterior를 근사합니다. (variational lower bound의 reparameterization)
이 논문에서는 Auto Encoding VB (AEVB) 알고리즘을 사용합니다. 이는 SGVB estimator를 사용하여 효과적으로 estimate 할 수 있습니다.
- 여기까지의 내용이 이해가 잘 안갈 수 있는데, 대충 Posterior를 이해하는 과정에서 통상 Evidence라고 불리는 것을 구할 때 어려움을 겪습니다. 이 Evidence에 Variational Inference를 적용하여 ELBO 라는 Variational Lower Bound를 알 수 있는데, 이 bound에 대하여 Stochastic Gradient를 통해 optimize 했다고 생각하시면 됩니다.
Method
Problem scenario
우선 문제에 대한 정의를 해보자.
그리고 위 Abstract에서 말했듯이 datapoints는 관찰되지 않은 연속적인 random variable
이 생성되는 process는 두 단계로 나눠지는데,
1)
2)
그리고
하지만 우리는 이 정보(Likelihood와 Prior)만을 가지고는 posterior와 evidence를 알 수 없습니다. 대신에 이를 efficiently learning을 해봅시다.
우리의 Solution
1. parameter
2. 주어진 data
3. data variable
사실상 위 세가지 솔루션은 Variational Inference를 통한 ELBO식을 통해서 효율적으로 근사가 가능합니다.
근데 앞서 말씀드렸다싶이, true posterior
Variational Bayesian의 대표적인 방법인 mean field approximation은 앞에서 언급했다싶이 intractable하거나 expensive computation을 갖게 되는데, 이 방법 대신
The variational bound

Evidence의 Lower bound를 구하는 방법엔 두가지 방법이 있는데, 첫번째는 위 사진의 Jensen's Inequality를 사용하여 구하는 방법이 있고,

두번째는 True Posterior를 근사하고자 하는 노력으로부터 시작하는 방법이 있습니다.
애초에 Evidence에서 시작하는 법으로 다양한 방법이 있는 것으로 압니다만 일단 이정도로 표기하겠습니다.


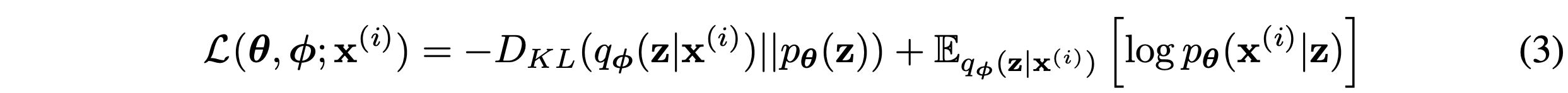
쨌든 저희는 위의 식 유도를 통해서 이 세가지 equation에 대한 이해를 마쳤습니다.
위에서 언급했듯이 저희는 Stochastic Gradient Descent 방법으로 Optimize를 할 것이기 때문에 주어진 Lower bound
하지만 여기에서 문제가 발생하는데, 보편화 된 표현으로 예를 들어 설명해보겠습니다.
만약
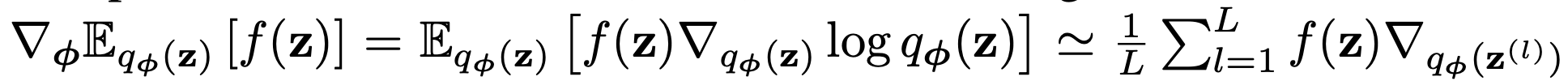
그럼 미분에 대한 표현이 이런식으로 진행이 되는데, 잘 살펴보시면 미분이 f(z)에 대해서 진행되지가 않습니다. 이런 요인 때문에 높은 Variance를 지니게 되는데요, 이를 해결하기 위해 reparameterization이 도입됩니다. (VAE에서 유연한 미분을 위해서도 적용이 되지만요.)
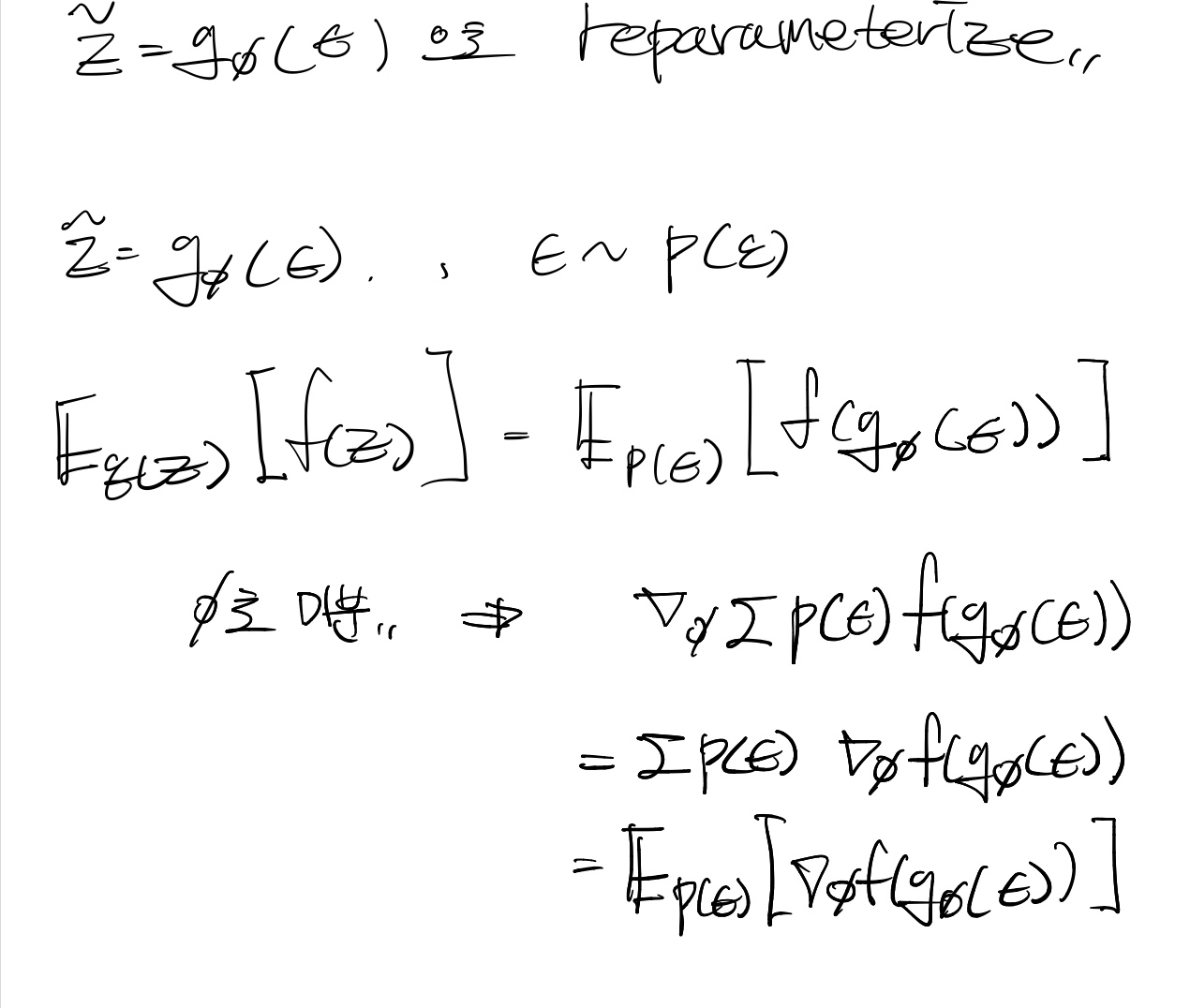
위의 식 전개를 보면, reparameterize 하면 비로소 주어진 함수 f()에 대해 미분이 됨을 알 수 있습니다.
이를 통해 높은 variance를 갖는 형태를 극복할 수 있습니다.
위 높은 variance를 갖는 미분 형식을 Likelihood-ratio gradient라고 합니다.
- 다음 포스트에 이어 적도록 하겠습니다.
'Generative Model' 카테고리의 다른 글
| Generating Diverse High-Fidelity Images with VQ-VAE2 (0) | 2021.09.20 |
|---|---|
| Neural Discrete Representation Learning : VQ-VAE (0) | 2021.09.17 |
| Variational Auto Encoder를 이해해보자! (3) (0) | 2021.09.14 |
| Variational Auto Encoder를 이해해보자! (2) (0) | 2021.09.13 |
| Denoising Diffusion Probabilistic Model : DDPM (1) | 2021.09.10 |



