Abstact
본 논문에서 제시하는 바는 다음과 같습니다.
1. G, D 사이의 Balance
2. Convergence Measure
3. Diversity, quality 의 조절
Proposed method
기존 GAN의 경우 Data Distribution을 Matching 하는데 중점을 두고 있습니다. 하지만 본 논문에서 제시하는 BEGAN은 AutoEncoder의 Loss distribution을 매칭합니다. 모델 자체는 저번 포스트에 언급한 EBGAN의 AutoEncoder를 차용합니다.
사실 Equilibrium term을 제외하면 EBGAN과 크게 다른점은 없습니다.
Wasserstein distance lower bound for auto-encoder
위의 식과 같이, 1 or 2 Wasserstein Distance로 Auto Encoder Output (Loss)를 지정합니다. L2 의 경우 기존 EBGAN의 MSE Loss와 동일한 형태가 됩니다.
\(\mu_1, \mu_2\)를 각각 Real Data Loss Distribution, Fake Data Loss Distribution이라 했을 때 Wasserstein Distance로 Loss Distribution을 Matching 하게 됩니다. 기존 GAN과는 달리 Loss distribution을 matching 하는 방식입니다.
Wasserstein distance로 최적화하는데 있어서 수식적으로 풀어나가보면, 두가지로 설명할 수 있습니다.
첫번째로는, 매우 제한된 상황에서 Frechet Distance를 사용하여 수식적으로 풀어나가는 방법이고
두번째로는, 단순히 Jensen's inequality를 사용하여 lower bound를 구하는 방법입니다.
1.
위의 식에서 알 수 있듯이, data가 normal distribution을 따를 때 Frechet distance로 normal distribution 간의 거리를 구할 수 있습니다.
근데 거리 식의 두번째 항을 첫번째 항으로 나눴을 때 단조함수이거나 상수인 경우, 첫번째 항만 optimize 할 수 있습니다.. 이와 같은 방법으로 wasserstein distance를 tractable하게 가져옵니다.
사실 이러한 조건들은 실제로 성립되기 너무너무 힘듭니다.
2.
위와 같이 Jensen's inequality를 통해 최적화 하는 방법도 존재합니다.
lower bound를 최적화하는 문제로 바뀌었지만, 그래도 첫번째 수식 전개 결과보다는 합리적입니다.
주목할 점은, WGAN과는 다르게 loss distribution을 matching 한다는 점이고, Kantorovich Rubinstein Duality를 사용하지 않아서 lipschitz constraint로부터 자유롭다는 점입니다. (lower bound 이긴 하지만,,,)
GAN objective
BEGAN은 위의 식인, wasserstein distance lower bound에 대해 최적화합니다.
Discriminator를 훈련할 때는 두 distribution을 멀게 해야합니다. 즉, 위의 wasserstein distance lower bound를 maximize 하는 방향으로 훈련해야합니다. 이 때, 식에 절대값이 있기 때문에 위의 a, b 처럼 두가지 경우로 나뉘게 됩니다.
\(\mu_1, \mu_2\)가 각각 real data loss distribution, fake data loss distribution이라 했을때, Energy 값의 경우 real에 가까울수록 작은 값이 나와야해서 b가 현재 컨셉에 맞습니다.
그래서 b를 사용합니다.
전체 Loss는 위와 같습니다.
이 식은 WGAN loss와 비슷하지만, 주의해야할 점은 위에서 언급했듯 WGAN과 다르게 Kantorovich Rubinstein Duality를 사용하지 않고 lower bound로 최적화하기 때문에 lipschitz constraint에 자유롭다는 것입니다.
그리고 data distribution을 matching하는 것이 아닌, loss를 매칭하게 된다는 것입니다.
Equilibrium
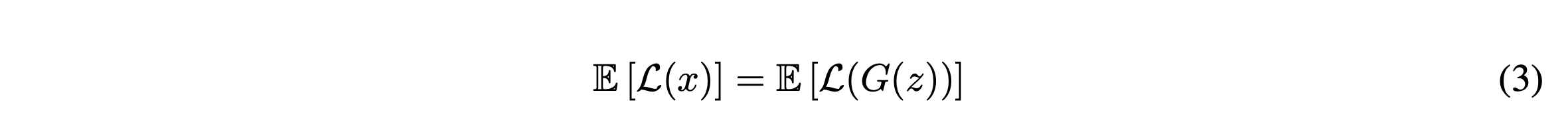
위의 식과 같은 평형을 유지하는 것이 굉장히 중요합니다.
이 때 0~1 사이의 값을 갖는 \(\gamma\) 라는 하이퍼파라미터를 제시합니다.
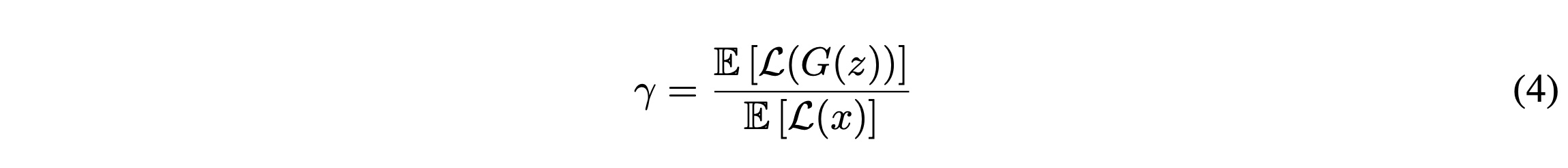
이 하이퍼파라미터는 데이터 생성의 목적성과 관련이 깊습니다.
\(\lambda\)가 작은 경우의 평형을 유지하도록 훈련하게 되면 이미지를 잘 Decoding을 하려고 하지만 Diversity에 있어서는 다소 약할 수 있고, \(\lambda\)가 큰 경우의 평형을 유지하도록 훈련하게 되면 이미지의 Diversity에 좀 더 주의를 기울일 수 있습니다.
Boundary Equilibrium GAN
위의 식을 사용하여 실제로 BEGAN을 훈련하게 됩니다.
이대로 훈련하게 되면 결국 아래와 같이 사용자가 설정한 Equilibrium을 이룰 수 있습니다.
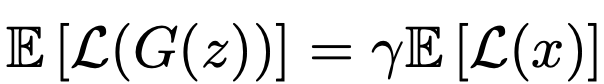
훈련 초반에는 Generator가 Reconstruction 하기 쉬운 data를 만들어내고, Discriminator는 Real Data에 대해 확실히 학습이 안됐기 때문에 \(L(x) > L(G(x))\) 가 됩니다. 그리고 위의 training process를 통해 서서히 위의 equilibrium을 만족하게 됩니다.
만약 훈련 중, Model Balance의 의도가 담긴 \(\gamma\) 기준에 벗어났다고 해봅시다.
그럼 두가지 상황이 있을 텐데,
1. Generator가 우세한 경우 -> k 값이 높다. -> Discriminator Loss 중 Generator를 견제하게 됌.
2. else. 반대.
이런식으로 훈련이 진행되게됩니다.
이때, k는 0, 1 사이의 값을 갖고 0부터 시작합니다.
Convergence Measure
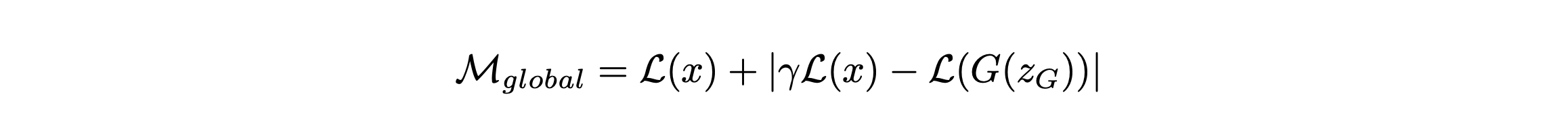
본 논문에서 convergence measure를 위의 equilibrium concept를 사용하여 제안합니다.
closest reconstruction \(L(x)\)와 lowest absolute value \(|\gamma L(x) - L(G(z))|\)를 사용하여 covergence measure를 측정하게 됩니다.
'Generative Model' 카테고리의 다른 글
| Subspace Diffusion Generative Models 설명 (0) | 2022.10.23 |
|---|---|
| EBGAN : ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS (0) | 2022.06.18 |
| NCSN : Generative Modeling by Estimating Gradients of the Data Distribution 리뷰 (1) (0) | 2022.05.24 |
| Improved Denoising Diffusion Probabilistic Models : Improved DDPM (0) | 2022.05.18 |
| StyleGAN3 : Alias-Free Generative Adversarial Networks (2) (0) | 2022.05.01 |
