DDPM을 개선시킨 논문을 발견하게 되어 공부하게 되었습니다. DDPM에 대해 한층 더 잘 알게된 경험이었어서 꼭 한번쯤 읽어보시는걸 추천드립니다 :)
Introduction
본 논문에서 제시하는 바는 3가지 입니다.
1. competitive log-likelihood
2. sampling 시 더 적은 diffusion step으로.
3. model scaling과 diffusion steps에 따라 sample quality와 log-likelihood가 어떻게 바뀌는지
이전 DDPM의 경우 image quality는 높았지만 log-likelihood 수치 자체는 그렇게 좋지 않았습니다. 이를 해결하기 위해 좀 더 나은 noise를 사용하고, 기존의 loss에 추가 term을 붙인 hybrid loss term을 제시합니다.
기존 DDPM에 대해 잘 모르신다면 https://deepseow.tistory.com/37 를 한번 읽어보시는걸 추천드립니다!
지금부터 기술하는 내용은 DDPM 프로세스를 잘 안다는 가정하에 작성하겠습니다 :)
Improving The Log-Likelihood
이전 연구들을 좀 살펴보면 Generative model에서 Log likelihood 지표가 상승했을 때 sample quality가 급격히 좋아지는 경우가 많았습니다. 그리고 보통 data distribution에 맞추는것이라고 여기기 때문에 log likelihood는 굉장히 중요한 metric 이라고 할 수 있습니다.
그러나 아쉽게도 기존 DDPM의 경우 Log likelihood 수치에 있어서는 competitive 하지 못했습니다. (image quality는 좋긴한데..)
이런 상황에서, DDPM이 왜 좋지 않은 Log likelihood를 내놓는지 확인 할 필요가 있습니다.
Learning \(\Sigma_\theta (x_t, t)\)
이에 앞서, 기존의 DDPM은 q의 posterior에 대해 variance를 \(\tilde \beta\)로 사용하나, \(\beta\)를 사용하나 비슷한 결과를 내놓는다고 했습니다.
이러한 결과는 경험적으로 얻어졌으나, 왜 이런 결과가 나오는지 다시 생각할 필요가 있습니다.
위의 Figure는 Diffusion step 크기에 따른 \(\tilde \beta\) \(\beta\)의 비율을 찍은 결과입니다.
Diffusion step이 커질수록 \(\beta\)는 \(\tilde \beta\)와 거의 비슷해집니다. 그래서 비슷한 결과를 내놓은거구요.
그래서 Diffusion step이 무한대에 가까워진다면 사실 동일해지겠죠??
근데 위의 사실이 log likelihood와 무슨 상관이 있을까요??
위의 Figure는 VLB, 즉 log likelihood의 ELBO에 해당하는 값이 diffusion step가 흘러감에 따라 어떻게 변하는지 보여줍니다.
즉, 초반 step에서 VLB가 급격히 떨어짐을 알 수 있습니다.
이를 통해 \(\Sigma_\theta (x_t, t)\)가 중요하다는 걸 알 수 있습니다.
근데 기존 DDPM의 경우는, t에 따라 결정되는 constant로 여겨서 훈련에 참여시키지 않습니다.
\(\Sigma_\theta (x_t, t)\)를 NN으로 훈련시켜서 막상 예측시키려해봐도 range가 너무 작아서 예측이 어렵습니다. 그래서 sigma를 내놓는 대신 vector v를 내놓게 해서 간접적으로 \(\Sigma_\theta (x_t, t)\)를 계산하게 합니다. 이 때 v 는 dimension 당 1개의 component를 갖습니다.
간접적으로 구하는 식은 위와 같습니다. (variance 끼리 log domain에서 보간.) 위의 식에서 v에는 딱히 별다른 제한은 없지만 실제로 훈련시켜보면 0~1 사이의 값을 갖게된다고 합니다.
보간을 하는 이유
왜 위처럼 보간하는 형태로 훈련을 진행할까요?
Diffusion models, Score matching 모델들의 시초라고 불릴 수 있는 "Deep Unsupervised Learning using Nonequilibrium Thermodynamics" 논문에서 위와 같은 관계가 성립함을 증명합니다.
근데 위와 같은 transition rule에 대한 entropy는 결국 gaussian 에 대한 entropy가 되고 이는 variance에 대한 식으로 나타내질 수 있습니다.
이를 기반으로 하여 위 (24)의 식을 풀어본다면 아래와 같은 관계가 성립하게 됩니다.
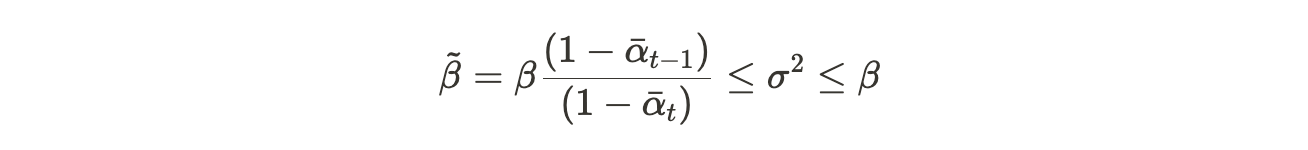
즉, (16) 식과 같이 보간 형태로 나타내는게 옳고 자연스럽게 v는 0~1 사이의 값을 갖게 됩니다.
근데 기존 DDPM의 Loss 인, \(L_{simple}\)은 \(\Sigma_\theta (x_t, t)\)를 훈련에 참여시키지 않기 때문에 직접적으로 VLB 를 Loss로 사용합니다.
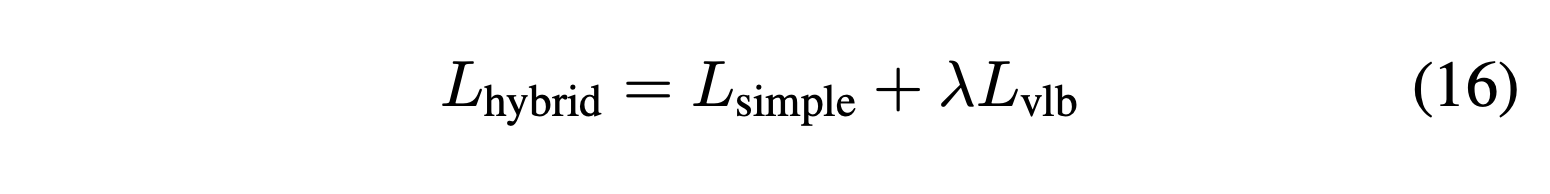
위의 식처럼요!
\(\lambda\)는 0.001로 사용합니다. 그리고 VLB Term에서 mean은 stop gradient를 적용합니다. 이를 통해 mean에 대해 주로 최적화를 진행하면서 Variance에 올바른 guide를 제시할 수 있게 됩니다.
Improving The Noise Schedule
기존 DDPM으로 ImageNet 64x64 데이터셋에 대해 훈련시켰을때 forward process (Noise를 더해가는 process)가 굉장히 noisy 하다고 합니다. 너무 과해서 sample quality를 보장할 수 없었습니다.
위의 Figure가 이를 잘 보여줍니다. 윗줄에 해당하는데, 굉장히 빠르게 noisy 하게 됨을 알 수 있습니다.
이러한 이유로 좀더 천천히 noise를 적용할 필요가 있습니다.
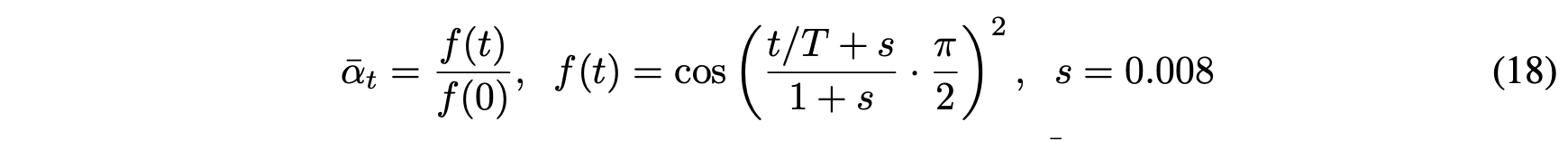
그래서 본 연구에서는 위의 식과 같이 cos 함수를 통한 cosine schedule을 제시합니다.
그리고 t = T 일 때 \(\beta\)의 크기가 0.999를 넘어가지 않도록 clipping 또한 적용해줍니다.
위의 Figure는 기존의 Linear schedule과 cosine schedule 사이의 차이점을 보여주고 있습니다.
schedule factor가 0에 가까워질 수록 이미지 파괴를 더 많이 시켰다는 뜻인데, linear의 경우 diffusion step 초, 중반 부분에서 노이즈를 과격하게 증가시키는 반면 cosine schedule의 경우 좀 더 완만하게 노이즈를 증가시킴을 알 수 있습니다.
Reducing Gradient Noise
Gradient Noise란 무엇을 의미할까요 ?
https://arxiv.org/pdf/1812.06162.pdf
보통 배치사이즈가 작으면 High variance를 갖기 때문에 true gradient와는 다소 다를 수 있습니다. 이런 경우 gradient noise가 크게 발생하게 됩니다.
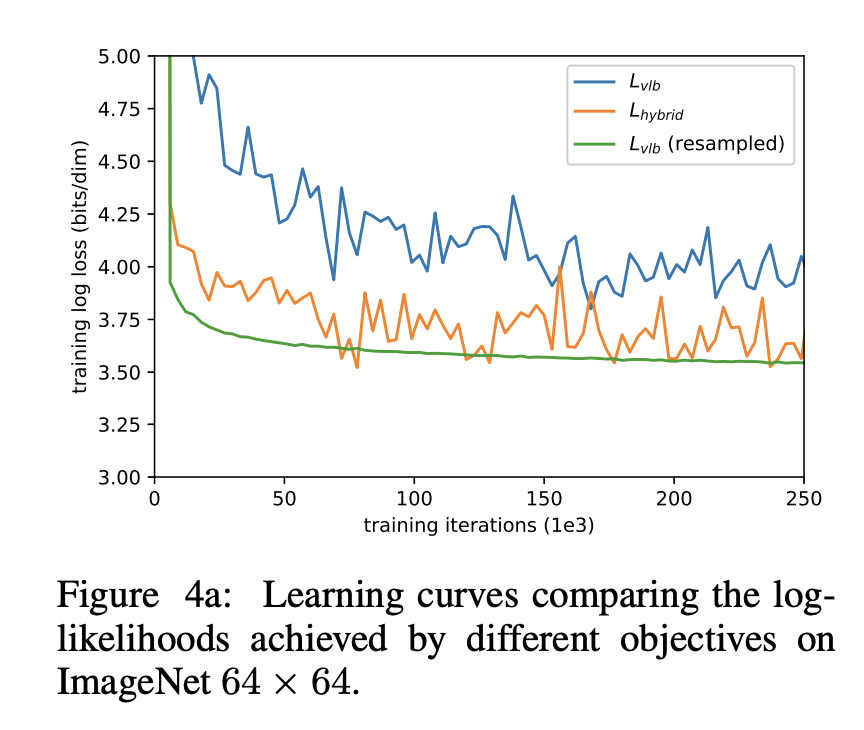
윗부분에서 제시한 VLB Term을 추가한 Hybrid Term과 VLB Term의 learning curve를 찍어본 결과 굉장히 noisy 하게 나옴을 알 수 있습니다. 하지만 Hybrid Loss가 더 높은 성능을 보이는 건 확실하구요.
본 논문에서는 VLB Loss Term이 Hybrid Loss Term보다 더 noisy하다고 가정했습니다. (Hybrid의 경우 성능 자체가 더 높았기 때문에.)
그래서 VLB Loss Term의 variance를 낮추는데 집중합니다. 근데 여기에서 왜 VLB Loss 의 variance가 높은걸까요?
이에 대해서는 훈련 시 t를 sampling 하기 때문이라고 가정합니다. 그래서 t에 대한 importance sampling 방법을 제시합니다.
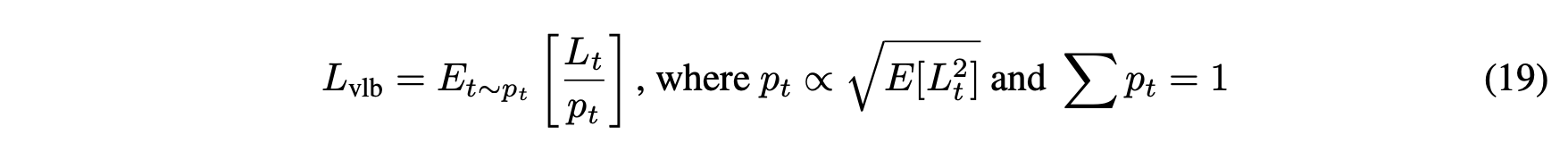
위의 식처럼 t의 확률 \(\p_t\)를 정하고 VLB loss 또한 p의 영향을 고려할 수 있게 수정해줍니다.
근데 처음 훈련할 때는 p에 대한 정보를 알 수 없습니다. 그래서 모든 \(t \in [0, T-1]\)에 대해서 10 sample씩 뽑을 때 까지는 단순 무작위로 돌리고 Loss value를 기억해둡니다.
그리고 그 정보를 통해 위의 importance sampling 방법을 적용합니다.
위 Figure 4a의 resampled curve가 이를 보여줍니다. (훨씬 더 smooth 해진 모습..)
Result
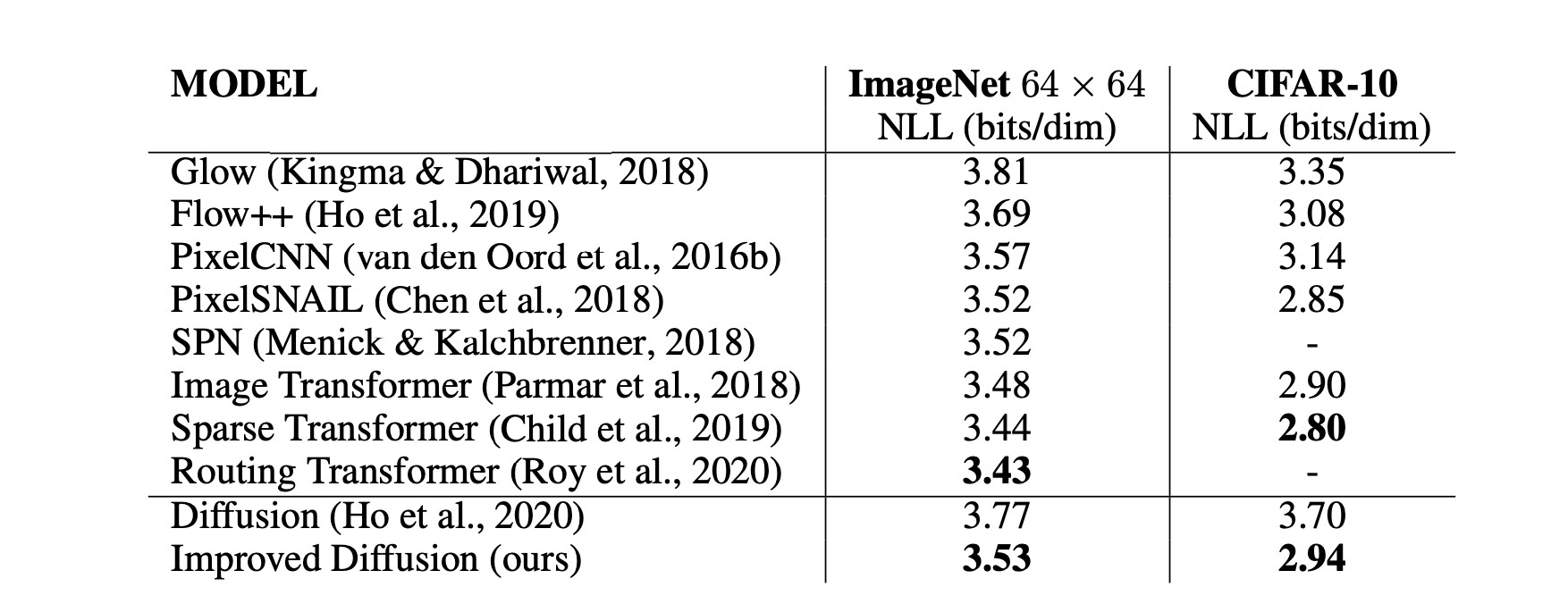
굉장히 훌륭한 NLL 수치를 보여줍니다.
Improving Sampling Speed
본 연구에서 제시하는 모델은 모두 4000 diffusion step으로 진행합니다. 근데 diffusion step이 굉장히 커서 최신 GPU를 사용하더라도 하나의 sample을 만드는데 몇분씩 걸리게 됩니다.
근데 Sampling 과정이 이미 훈련시켜놓은 pre-trained model로 복원하는 것이기 때문에 더 적은 diffusion step으로도 high quality sample을 뽑아 낼 수 있습니다.
그래서 모든 diffusion step을 사용하는게 아닌 strided diffusion step으로 진행하게 됩니다.
S = (1, 3, 5, ..., T − 1) 이런식으로요!
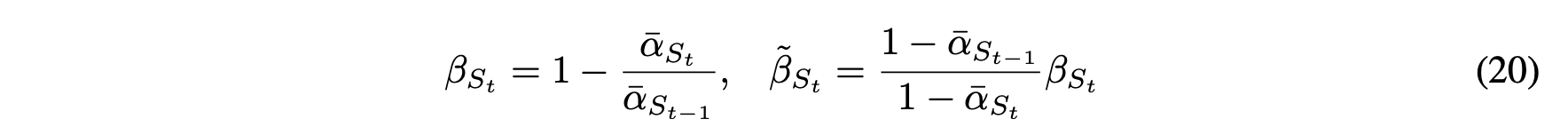
그럼 위처럼 noise schedule을 strided step으로 가져오게 되고, 이를 통해 DDPM sampling을 진행합니다.
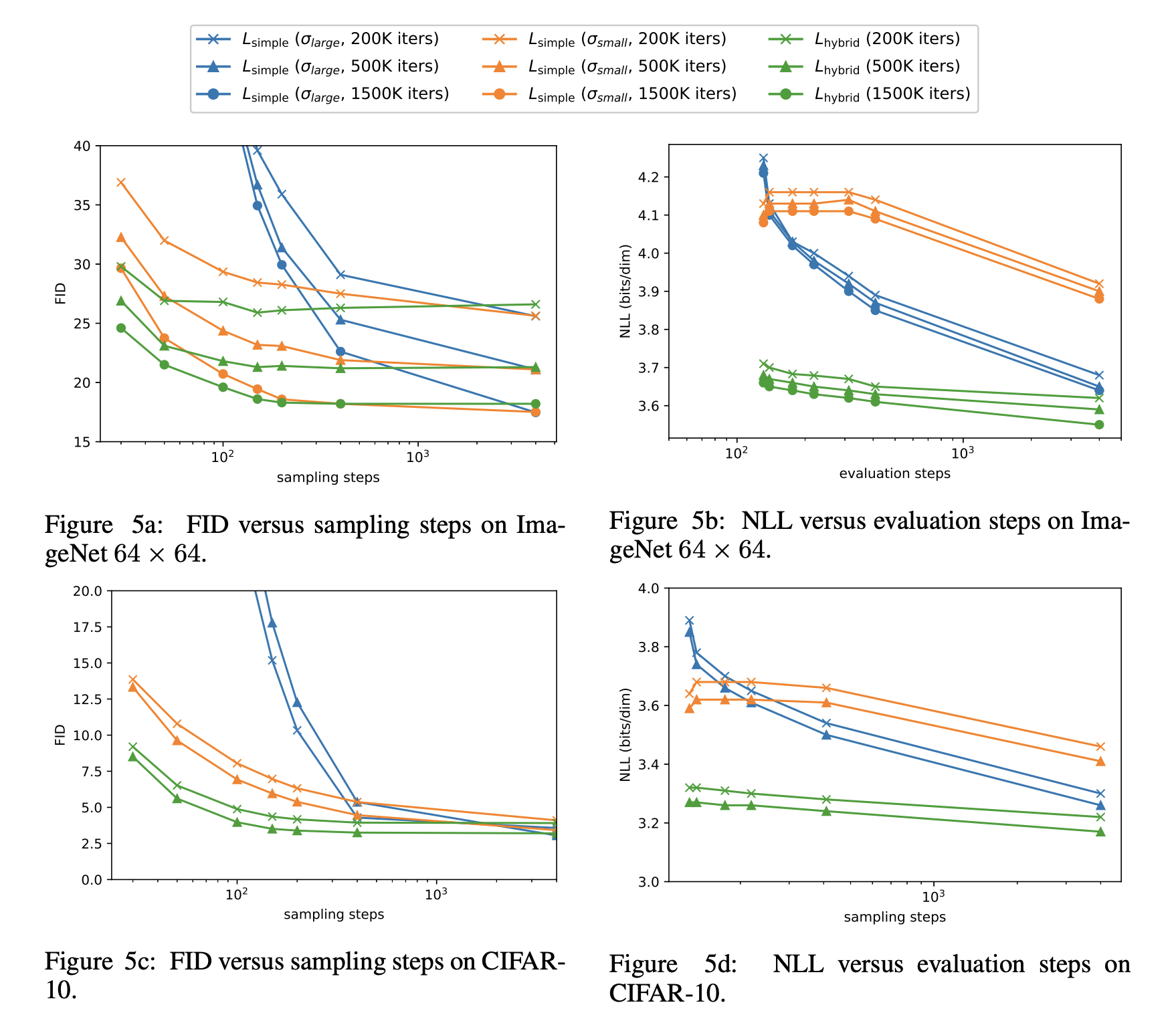
stride는 Diffusion step을 sampling step으로 나누면 됩니다. 위 Figure는 sampling step에 따른 성능 변화를 보여줍니다.
Scaling Model Size
NLL 성능을 높이기 위해 위의 방법들 뿐만 아니라, Model size 자체를 키우는 방법 또한 제시합니다.
사실 ImageNet과 같이 다양한 이미지가 들어있는 데이터셋의 경우 model capacity가 더욱 중요합니다.
GAN에 대한 연구이긴 하지만 아래 연구에서도 이러한 방법을 사용합니다.
https://arxiv.org/pdf/2202.00273.pdf
본 논문에서는 모델 사이즈에 대해서는 경험적으로 연구를 진행했는데, 모델 사이즈에 따라 ImageNet 64x64 데이터셋에 대한 성능을 측정했습니다.
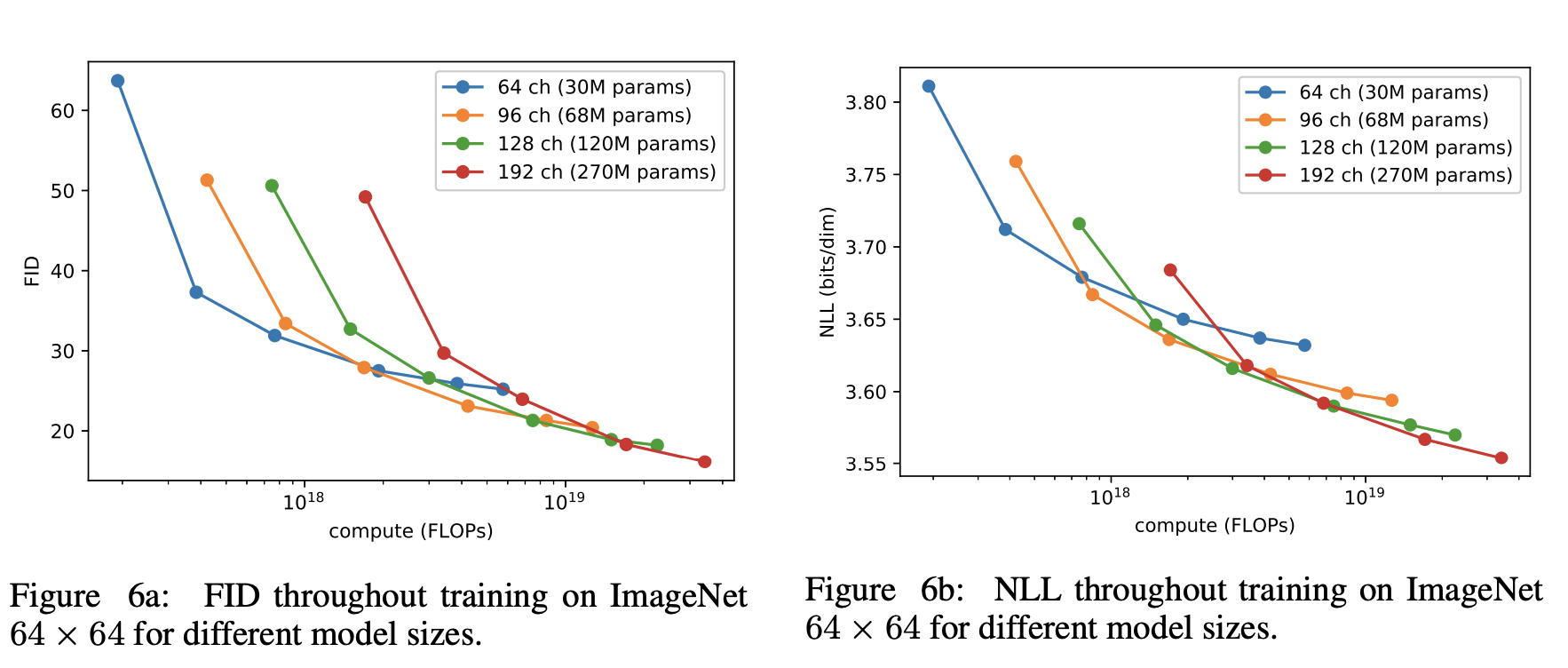
확실히 모델 사이즈가 커질 수록 더 높은 성능을 보임을 알 수 있습니다.
'Generative Model' 카테고리의 다른 글
| EBGAN : ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS (0) | 2022.06.18 |
|---|---|
| NCSN : Generative Modeling by Estimating Gradients of the Data Distribution 리뷰 (1) (0) | 2022.05.24 |
| StyleGAN3 : Alias-Free Generative Adversarial Networks (2) (0) | 2022.05.01 |
| StyleGAN3 : Alias-Free Generative Adversarial Networks (1) (0) | 2022.04.24 |
| StyleGAN2 : Analyzing and Improving the Image Quality of StyleGAN (0) | 2022.04.21 |
