시작하면서...
이 논문은 Feedback Network를 이용한 SR을 제시하는데, 처음 시작 할 때 Feedback Network가 뭔지도 잘 모르고, 제가 평소에 잘 사용하지 않는 RNN 형식을 사용하기 때문에 이해 자체가 어려웠었습니다. 하지만 읽다보니까 진짜 신기하고 신박한 내용이어서 공부하길 잘 했다는 생각이 듭니다 ㅎㅎ..
Abstract
최근에 CNN, GAN 등 여러 모델에 대한 SR 방법들을 통해 SR에 대한 발전이 꾸준히 이뤄지고 있습니다.
하지만 Feedback Network를 이용한 SR 방법에 대해서는 개척이 되고 있지 않습니다.
그래서 이 논문에서는 Feedback Network를 이용한 SR 방법인, SRFBN(Image Super Resolution FeedBack Network)을 제시합니다.
SRFBN은 RNN의 hidden states를 사용하여 feedback manner를 만족시킵니다.
Feedback Block
- handle feedback connection
- 강력한 generate HR
Introduction
지금까지 리뷰했던 SRCNN, SRGAN과 같은 Deep Learning을 이용한 SR Method 논문들을 보다보면 꼭 나오는 SR의 성질이 있습니다. 그건 바로 ill-posed입니다.
ill-posed : 초기의 아주 작은 변화에도 최종 결과가 많이 바뀔 수 있는 특성
이제 이 문제를 해결하기 위해 여러 방법들인 interpolation-based methods, reconstruction-based methods, learning-based methods 등 과 같은 방법들이 연구되어 왔습니다.
이 방법들 말고 Deep Learning을 이용한 방법을 제시하는데, Deep Learning을 방법으로 했을 때 좋은 이유가 두가지 있습니다.
- Depth
- Skip Connection
하지만 위 두가지 이유 중 Depth가 깊어지고, parameter의 수가 많아지다 보면 오버피팅이 발생하게 됩니다.
위와 같은 네트워크의 파라미터 문제를 줄이기 위해서 Recurrent structure를 사용합니다.
feedback machanism
이제 널리 사용되는 딥러닝 모델들과 비슷하게, RNN 또한 feedforward 에서 information들을 공유 할 수 있습니다.
하지만 feed forward manner는 skip connection을 사용하더라도 이전 레이어의 유용한 정보에 접근하는 것이 불가능합니다.
그래서 feedback manner를 사용하기로 합니다. feedback manner에서는 High level information을 low level infomation으로 가져와서 이전 레이어의 low level information을 조정하는게 가능합니다.
SRFBN에서 feedback machanism은 top-down(하향식)으로 작동합니다.
논문에서는 위의 내용을 아래처럼 기술합니다.
The feedback mechanism in these architectures works in a top-down manner, carrying high-level information back to previous layers and refining low-level encoded information
SRFBN에서는 feedback block(FB)을 포함하는 RNN을 사용합니다.
FB에서는 강력한 HR generation을 위해 dense skip connection(concat을 통한 skip connection)을 통한 upsampling, downsampling이 둘 다 이뤄집니다.
사실 위의 말이 처음 보면 와닿지 않고 이해가 되지 않습니다. 하지만 나중에 architecture를 보면 이해가 됩니다 ㅎㅎ
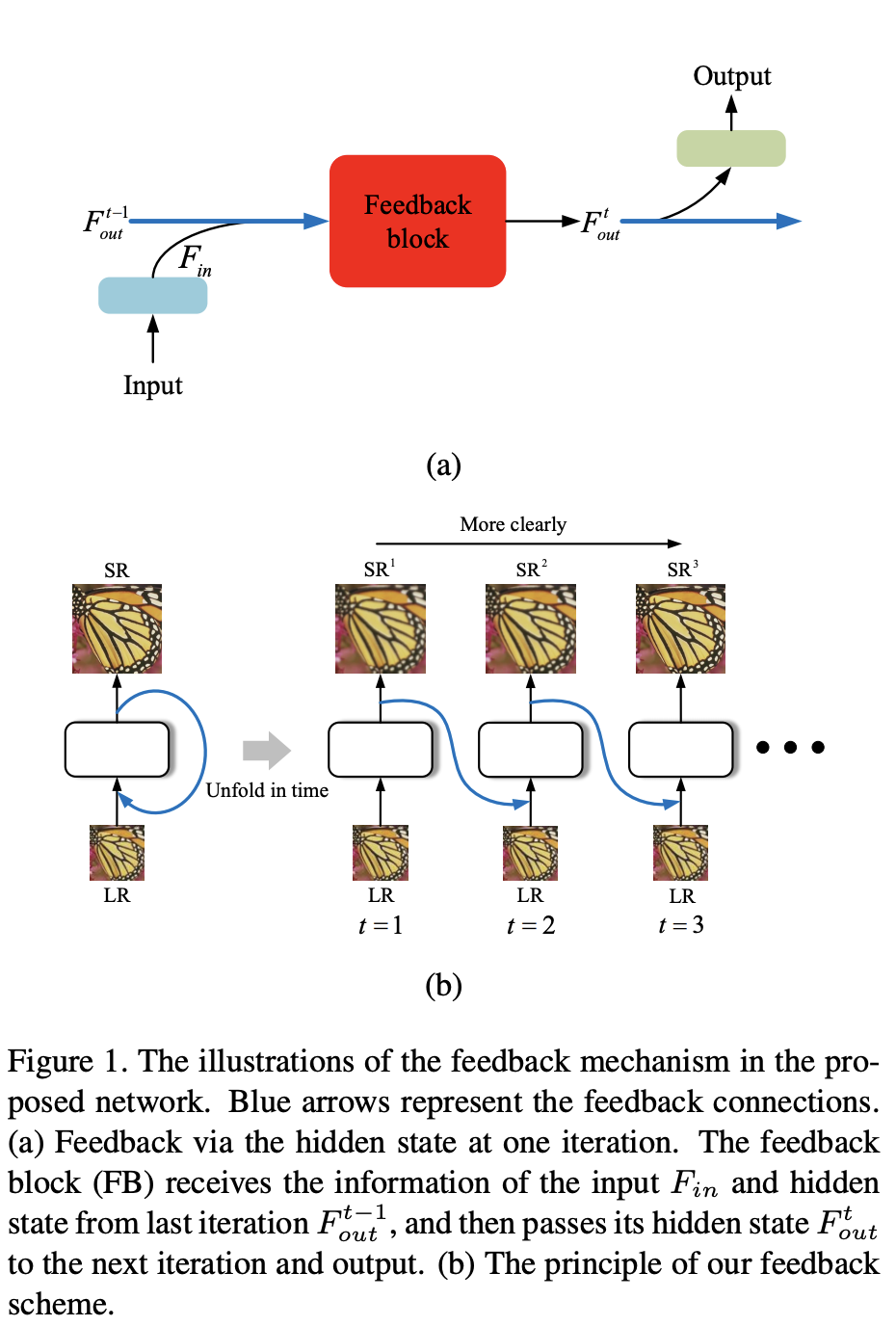
우선 이해를 돕기 위해 논문의 Fig. 1. 사진을 첨부했습니다.
loss
HR에 대한 정보를 hidden states가 갖게 하기 위해서 각 iteration간의 loss를 연결합니다.
To ensure the hidden state contains the information of the HR image, we connect the loss to each iteration during the training process
저도 이 말의 뜻을 이해를 잘 못하겠는데, 제 생각에는 SRFBN에서는 iteration이라는 표현을 RNN에 대해 다음 hidden states로 옮겨가는 그 부분을 뜻하는데 사용하는데, 이제 RNN을 이용한 architecture에서 hidden states간의 연결을 고려해서 loss를 묶는 다는 뜻 같습니다.
이제 SRFBN이 RNN의 형태만 가져와서 hidden 부분에 Feedback Block을 놓은 형태이기 때문에, 기존의 프레임워크에서 지원하는 RNN이라면 loss가 자연스레 연결이 되는게 당연하겠지만 이 논문에서의 SRFBN은 각 한 부분의 sub network를 연결해 직접 구성해야되서 위처럼 언급한게 아닐까 싶습니다.
Related Work
Feedback Mechanism
feedback mechanism은 이전 상태에 대한 정보를 운반을 가능하게 하는 mechanism이라고 생각하시면 됩니다. (논문에서의 개조된 RNN)
지금까지 feedback mechanism을 이용한 방법들이 많이 연구되고 나왔었지만 이 방법들은 결국 LR에서 SR image 까지 feed forward로 정보를 보냅니다.
하지만 이 논문에서는 Feedback Mechanism에 맞추기 위해 Feedback Block을 사용합니다.
그리고 FB 안에서 효과적으로 정보를 보내기 위해 Dense skip connection을 사용합니다.
Dense skip connection은 Densenet을 공부하시면 알 수 있습니다. 간단하게 말하면 Resnet에서 Add 부분을 Concat으로 바꿨다고 생각하시면 됩니다.
Curriculum Learning
Curriculum Learning이란 target에 대한 훈련 난이도를 점진적으로 올리는 것을 말합니다.
SRFBN에서는 RNN 형식을 이용하여 T iteration 만큼 점진적으로 훈련시킵니다.
Feedback Network for Image SR
feedback system에는 두가지 조건이 있습니다.
- iterativeness
- 시스템의 output 경로 변경
반복적인 원인과 결과의 procss는 feedback의 원리를 갖도록 해주고, high level information에 더 나은 SR Image를 만들 수 있도록 도와줍니다.
이 네트워크에서 가장 필수적인 세가지가 존재하는데, 이는
- 각 iteration에 대한 loss 를 묶기(hidden state가 high level information을 보낼 수 있도록)
- RNN 사용
- 각 iteration마다 LR Image 제공
Network Structure
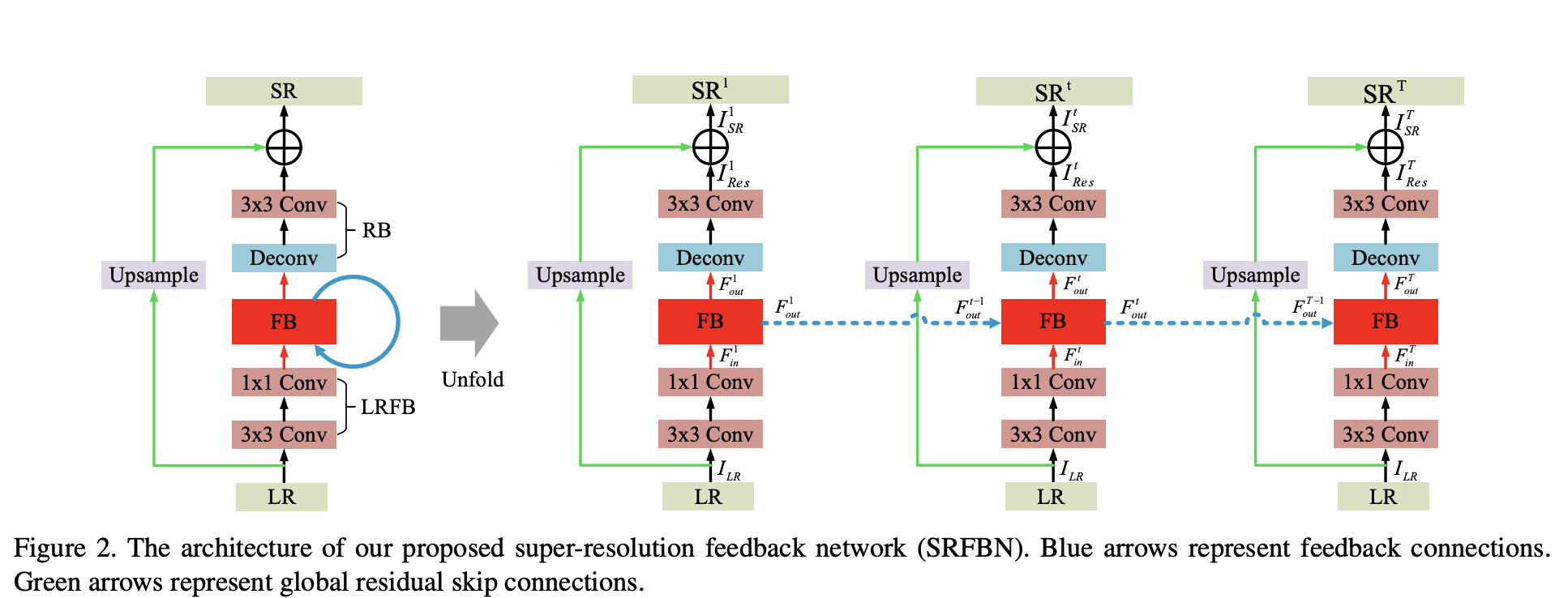
위 Fig. 2.을 보시면 아키텍쳐가 세 부분으로 나눠져 있는 것을 알 수 있습니다.
- LR feature extraction block(LRFB)
- Feedback block(FB)
- Reconstruction block(RB)
아키텍쳐에서 각 block의 가중치들은 시간에 걸쳐 공유되고 global residual skip connection가 존재 합니다.
global residual skip connection은 input LR image에 대한 residual image \(I^t_Res\)를 recover 하는데 목적을 둡니다.
LRFB
LRFB(LR feature extraction block)은 \(Conv(3,4m), Conv(3,m)\)을 포함하고 있습니다.t interation에 대한 LR input에서 shallow features인 \(F^t_{in}\)을 output으로 갖습니다.
$$
F^t_{in} = f_{LRFB}(I_{LR})
$$
FB
t iteration에 대한 FB(Feedback block)은 이전 iteration에 대한 hidden state \(F^{t-1}_out\)와 shallow feature인 \(F^t_in\)이 Input으로 들어갑니다.
$$
F^t_out = f_FB(F^{t-1}_out, F^t_in)
$$
RB
RB(Reconstruction Block)은 \(Deconv(k,m), Conv(3,c_{out})\)으로 이루어져 있고, 각각은 FB의 Output \(F^{t}{out}\)에 대한 Upscaling, 그리고 Residual Image \(I^{t}{Res}\)를 생성합니다.
$$
I^t_{Res} = f_{RB}(F^t_{out})
$$
Residual Skip Connection
$$
I^t_{SR} = I^t_{Res} + f_{UP}(I_{LR})
$$
bilinear upsampling 된 \(I_{LR}\)와 \(I^t_Res\)의 Skip Connection을 의미합니다.
T iteration 이 후 SR images (\(I^1_SR,I^2_SR,...,I^T_SR\))를 얻습니다.
Feedback block

Fig. 3.을 보면 좀 이해하기 힘든 구조로 되어있습니다.
t iteration에서의 FB(feedback block)은 \(F^{t-1}_out\)과 \(F^t_in\)을 concat한 것을 input으로 받습니다.
FB는 G개의 projection(dense skip connection) group을 갖습니다. 각 projection group에서는 upsample, downsample operation을 포함합니다.
FB가 시작하면서 \(F^{t-1}_out\)과 \(F^t_in\)을 concatenate 시키고 \(Conv(1,m)\)를 통해 압축 시킵니다.
$$
L^t_0 = C_0([F^{t-1}_out,F^t_in])
$$
위의 식에서 \(C_0\)은 compression and concatenation을 뜻합니다.
그리고 L에 대한 t iteration의 cocatenation들에 대해서 upsampling 해줍니다.
$$
H^t_g = C^\uparrow_g([L^t_0,L^t_1,...,L^t_{g-1}])
$$
\(C^\uparrow_g\)은 \(Deconv(k,m)\)을 통한 upsampling을 의미합니다.
이와 대응되게, \(L^t_g\) 또한 다음과 얻어집니다.
$$
L^t_g = C^\downarrow_g([H^t_0,H^t_1,...,H^t_g])
$$
\(C^\downarrow_g\)는 \(Conv(k,m)\)를 통한 downsampling을 의미합니다.
그리고 \(C^\uparrow_g\), \(C^\downarrow_g\)를 수행하기 전에 \(Conv(1,m)\)을 적용해줘서 parameter와 계산의 효율성을 높여줍니다.
$$
F^t_{out} = C_{FF}([L^t_1,L^t_2,...,L^t_G])
$$
여기에서 \(C_{FF}\)는 \(Conv(1,m)\)을 의미합니다.
Curriculum learning strategy
loss를 L1 loss를 사용합니다.
T개의 multiple output과 점진적으로 난이도가 증가하는 \(I^1_{HR},I^2_{HR},...,I^T_{HR}\)를 L1 Loss 적용
$$
L(\Theta) = {1 \above 1pt T}\sum^T_{t = 1}W^t||I^t_{HR}-I^t_{LR}||
$$
\(W^{t}\)는 t번쨰 iteration의 output에 대한 중요도? 가치 상수 입니다. 논문에서는 모든 iteration의 output의 가치를 동일하게 매겨서 1로 설정했습니다.
Implementation details
각 Sub-Network의 마지막 레이어 제외하고 Acitvation function으로 PReLU 사용했습니다.
x2, x3, x4 scale에 대해 Conv, Deconv의 하이퍼파라미터 k가 각각 다 다릅니다.
- x2 scale의 경우 k = 6, stride =2, padding =2
- x3 scale의 경우 k = 7, stride =3, padding =2
- x4 scale의 경우 k = 8, stride =4, padding =2
Experimental Results
training Dataset으로 DIV2K, Flick2k를 사용했고, 이전 포스트의 EDSR때와 동일한 Image Augmentation을 적용했습니다.
평가에 있어서는 전형적인 벤치마크 데이터셋인 Set5, Set14, B100, Urban100, Manga109에 대해 PSNR, SSIM을 기준으로 했습니다.
Study of T and G

m = base 32
T와 G의 값에 대해 고려를 해봐야하는데, T = 4, G = 6 일 때 성능이 가장 괜찮았었습니다.
Review
이렇게 Downsample, Upsample이 유기적으로 얽혀 있고, RNN의 형태만 가져와서 Feedback manner로 훈련시키는 모델을 처음 접했었기 때문에 좀 당황스럽기도 했고 이해하기가 많이 힘들었습니다.
하지만 노력을 들여서 이해하고 나니 이해하기 힘들었던 만큼 특이했던 구조가 너무 신기했고 이런식으로 생각을 할 수도 있구나 라고 생각이 들었습니다.



