StyleGAN XL 에 대한 포스트를 작성하면서 이전에 공부했었던 StyleGAN 시리즈에 대해 정리하면 좋겠다는 생각했습니다.
앞의 포스트에서도 언급했듯이, 이 시리즈를 쭉 읽어나가면서 많은 인사이트를 얻을 수 있었습니다. :)
Abstract
본 모델의 가장 핵심이 되는 컨셉은 Style Transfer의 요소를 적용했다는 것 입니다.
무엇보다 저는 제어 가능한 GAN 모델에 한 발자국 다가갔다는 점이 메리트가 있다고 생각합니다. Generator를 변경해서요!

Properties of the style-based generator
Style-based generator
Style transfer 요소를 가져온 Style-based generator란 무엇을 의미하는 걸까요?
위의 아키텍쳐를 보면 이해에 도움이 될거라 생각합니다! 원래 standard한 generator의 경우 보통 무작위적인 latent code를 input으로 넣어서 이미지를 만들어내는데요, StyleGAN의 아키텍쳐는 조금 다르다는 것을 알 수 있습니다.
latent code가 어떤 mapping network \(f\)를 통해 w라는 벡터로 변환됩니다. 이 벡터를 또 다른 affine transformation을 통해 \(y_s, y_b\) 라는 벡터로 만들어줍니다.
이 두 벡터를 통해 Generator에서 생성되고 있는 feature map에 AdaIN 작업을 진행해줍니다.
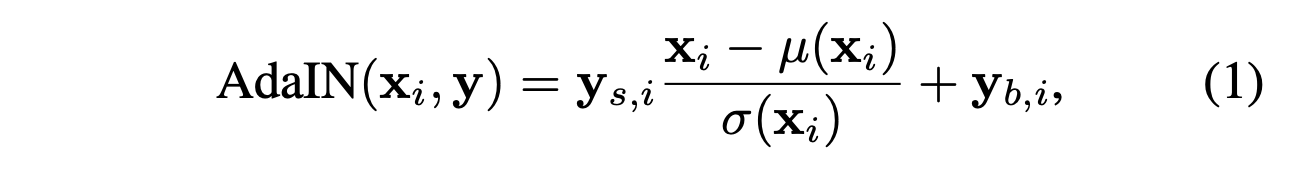
위의 식이 AdaIN에 대한 수식입니다. i는 channel index입니다. 식을 자세히 보시면 input x를 표준화 시키고 style code를 통해 통계적 특성을 변화시켜줍니다.
즉, channel에 대해 본 input의 분포를 변화시켜준다고 생각하면 될 것 같습니다.
주어진 input을 들어온 style을 통해 변화시켜준다! 직관적으로는 이렇게 이해하면 되겠네요.
그리고 또 특이한 점은 image를 생성해낼 때 4 x 4 x 512 shape의 constant로 시작한다는 것입니다. style과 중간의 noise injection에서 무작위성을 부여해주기 때문에 상수로 시작해도 문제가 없습니다.
Style Mixing
mapping network와 affine transform을 통해 학습된 distribution 기반 스타일을 통해 이미지를 그려낼 수 있습니다. 이를 통해 적절한 image generation을 진행할 수 있게 됩니다.
이 style은 stage 마다 적용이 되는데 이를 통해 localize 되어 style을 적용이 될 수 있습니다.
이를 통해 image의 certain aspects에 영향을 미칠 수 있구요. 특정한 aspects에 영향을 미친다는 것은 predictable 일 수 있다는 거고, 제어 가능한 GAN 모델에 한 발자국 더 다가갔다고 할 수 있겠네요!
이와 같이 localization 특성은 매우 중요합니다. 이러한 localization을 더 강화시키기 위한 style mixing 방법을 제안합니다.
두가지 latent code \(z_1, z_2\)를 통해 \(w_1, w_2\) 벡터를 만들어 냅니다. 이 후 초반엔 \(w_1\)을 사용하고 특정 crossover point를 기점으로 \(w_2\) 벡터로 바꿔 사용합니다. 이러한 과정을 Style Mixing 이라고 말합니다.

주목해야 할 점은 crossover point를 어느 지점으로 정하냐에 따라서 style이 미치는 영향이 달라지는데요.
위 Figure는 source A, B에 대한 latent vector를 style mixing 한 결과 입니다
coarse style은 초기 레이어에서 crossover point를 지정한 것이고 fine은 후반 레이어를 crossover point를 지정한 결과입니다.
Coarse Style Mixing의 경우 초반에 style의 변화가 있었기 때문에 큰 변화가 있었음을 알 수 있습니다.
Fine Style Mixing의 경우는 후반부에서 style 바꿨기 때문에 머리 색과 같은 미세한 변화가 있었음을 알 수 있습니다.
Stochastic Variation
본 논문에서 말하는 Stochastic Variation이란 바뀔 수 있는 미세한 요소들을 의미합니다. 예를 들어 사람 초상화의 경우 머리카락의 위치가 될 수 있겠네요!
이러한 Stochastic Variation에 영향을 미치는 것은 중간 중간의 Noise Injection 부분입니다. (노이즈 집어 넣는 것)
앞서 Style의 경우 input의 channel에 대해 통계량을 바꾸는 역할이었기 때문에 Global한 영향을 담당하고, 무작위적인 Noise의 경우 단순히 주입되는 것이기 때문에 미세한 부분을 바꾼다고 볼 수 있습니다.

위의 Figure는 noise만 다르게 했을 때의 결과물 입니다. 이 결과 머리카락의 위치와 같은 부분만 변화함을 알 수 있습니다.
Disentanglement studies
StyleGAN의 큰 특징은 제어 가능한 GAN에 한발자국 더 다가갔다는 점입니다. 이를 위해서는 지금까지의 특성들로는 다소 부족할 수 있습니다. 그 이유는 Disentanglement가 만족해야하기 때문이죠.
여기에서 Disentanglement를 만족한다는 것은 저희가 generator에서 linear interpolation을 진행했을 때를 생각하면 이해하기 쉽습니다.
두 latent code를 linear interpolation을 통해 새로운 하나의 latent code를 만들었다고 했을 때 predictable 하기 위해서는 latent space가 linear 해야함을 의미합니다.
실제로 모델에 주입되는 input은 style이라고 할 수 있는데 만약 latent code를 그대로 style로 사용한다면, latent space 자체는 무작위적인 얽혀있는 공간이기 때문에 disentanglement를 만족하기 어렵습니다.
그렇기 때문에 실제로 input으로 들어가는 style의 경우 얽혀있는 공간을 풀어줘서 만들어 줄 필요가 있습니다. 이를 위해서 여러 층의 mlp를 통해 curved한 latent space를 좀 더 linear하게 풀어줍니다. 이러한 과정을 unwarping 이라고 합니다.
Perceptual Path Length
위와 같이 linear interpolation을 거칠 때 predictable 한 것을 Disentanglement라고 한다면, 실제로 linear interpolation을 적용했을 때 지각적으로 자연스럽게 변화해야합니다.
이를 수치화 시킨 것이 Perceptual Path Length 입니다.
이를 위해 Perceptual based pairwise image distance를 사용하는데, 이는 VGG16 모델을 통해 두 이미지를 임베딩 시키고 거리를 구하는 것을 의미합니다.
이를 위해 두 latent code를 interpolation 시키는데 이 때 지점을 살짝 옮겨 두개의 결과를 만들어냅니다.
이 두개의 결과를 가지고 Perceptual distance를 구하면됩니다.
이 때 100,000 개 samples를 가지고 기댓값을 계산하면 됩니다.
\(\epsilon = 1e-4\), distance는 quadratic 하기 때문에 크기를 고려햐여 앞에 엡실론의 제곱분의 1로 나눠줍니다.

latent code에 대해서는 구형 선형보간을 적용합니다. (normalized input latent space에서는 구형 선형보간이 적절하다.)

그리고 w 벡터는 unwarp 된 상태이기 때문에 단순한 선형보간을 적용해줍니다.
Linear Separability
만약 latent space가 충분히 disentangle 되어 있다면 각 특성에 대해 linearly separable 할 것입니다.
linearly separable하다는 것은 Hyperplane으로 분리가 가능하다는 뜻입니다.
그럼 SVM 모델로 잘 분리가 되는지 보면 되겠네요!
그래서 본 논문에서는 linear SVM을 가지고 latent space point z and w를 예측하는 작업을 거칩니다.
우선 Linear Classifier로 20만 장의 생성된 이미지 분류 후 신뢰도가 높은 10만개의 이미지를 선택합니다. 여기에서 이미지 분류 기준은 CelebA라면 40개의 binary attribute가 됩니다.
이와 같은 과정을 통해 선택된 이미지들에 대응하는 latent vector z or w를 LinearSVM에 fitting 시킵니다. 이를 통해 Conditional Entropy를 계산합니다.
\(exp(\sum_i H(Y_i|X_i))\) : x가 들어왔을 때 true class에 대한 entropy가 얼마나 높은지 측정. 여기에서 i 는 Attribute에 대한 index가 됩니다.
이를 통해 LinearSVM 모델을 가지고 특정 클래스로 분류하기 위해 feature가 얼마나 부족한지 정량적으로 나타낼 수 있습니다. 낮을 수록 Linear Separability가 좋습니다!
Truncation trick in \(W\)
training data를 생각해봤을 때 low density 영역에 대해서는 generator가 훈련하기 어렵습니다.
이러한 단점을 해결하기 위해 w vector에 대해 mass의 중앙값을 계산하여 이를 변경시켜 사용합니다.
\(\hat w = E_{z \sim P(z)}[f(z)]\) 는 mass의 중앙값 입니다.
$$ w^{'} = \hat w + \psi (w-\hat w) $$
위의 벡터 \(w^{'}\)를 사용하면 됩니다.



