z [논문 리뷰] DETR : End-to-End Object Detection with Transformers
본문 바로가기
Computer Vision

[논문 리뷰] DETR : End-to-End Object Detection with Transformers

yhyj1001 2021. 5. 21. 10:49
728x90

Attention 및 Transformer에 대한 대략적 공부를 하시고 보는 것을 추천드립니다.
Panoptic segmentation은 고려되지 않았습니다.
Github : https://github.com/yhy258/DETR-For-Study

Abstract

이전의 object detection 방법들은 완전한 end-to-end하다고 할 수 없습니다. 그 이유는anchor box를 지정해준다던지 NMS를 통해 더 걸러낸다던지 사람이 상당히 많이 개입하는 부분들이 있기 때문입니다.


그래서 본 논문에서는 특정 매칭 방법을 이용한 이분 매칭을 통해 set prediction을 진행합니다. set prediction은 기존의 Object Detection에서 많은 Bounding Boxes를 detection 후 겹치는 것들은 NMS를 사용해서 걸러낸 것과 달리 애초에 겹치지 않는 하나의 set으로 예측하는 것이라고 생각하면 될 것 같습니다.


이러한 작업들을 가능하게 하는 encoder-decoder architecture의 DEtection TRansformer : DETR 을 제안합니다.

Introduction




Abstract에서 언급 했듯이 완전한 End-to-end를 제공하기 위한 architecture 입니다.
이를 위해 direct set prediction problem의 관점으로 pipeline을 간소화합니다.
이는 predicted & ground-truth 간의 이분매칭 작업을 넣음으로써 NMS, Anchor 등 여러 hand-designed component를 없앴습니다.

 

Fig 1.를 보시면 DETR의 간단한 형태가 나와있는데 transformer encoder-decoder를 거치고 이에 대한 output들에 대해 class와 bounding box를 예측합니다.





이분매칭은 위 사진과 같은 상황인데 set prediction을 진행하게 된다면 예측에 대한 순서가 ground truth와 맞지 않게 됩니다.


그래서 이분매칭 알고리즘을 통해 두 point 사이의 error를 최소화 하는 방향으로 매칭하게 됩니다.

The DETR model

이 architecture의 direct set prediction에 있어서 중요한 부분이 두가지 있습니다.

  1. set prediction loss를 통해 predicted와 ground truth 사이의 unique matching을 가능하게 한다.
  2. architecture는 single pass로 objects의 set을 예측하고 (set prediction) 그들의 relation의 관계를 파악합니다. (Attention)

Object detection set prediction loss

우선 DETR은 몇개를 탐지할 것 인지에 대해 정해줘야 합니다. 이 갯수는 실제 예측하는 object 수보다 충분히 크게 정해줍니다. 이를 N이라 notation 하겠습니다.

Hungarian Algorithm

loss의 첫 단계로,
predicted와 ground truth 사이를 unique matching 시키는 Hungarian algorithm이 있습니다.





이는 위 식처럼 표현 할 수 있습니다. 사실 위 식을 해결하는 방법으로 Hungarian algorithm을 사용합니다.
https://www.youtube.com/watch?v=cQ5MsiGaDY8
이에 대해서는 위 유튜브로 시청하시면 좋을 것 같습니다.


간단히 설명드리면 매칭 시켜야하는 두 factors에 대해 관계를 나타낼 수 있는 간단한 테이블을 그리고, 서로의 관계 즉 loss를 적습니다.


$$
l_{i,j} = l_{i,j} - min(l_i)
$$


이제 여기에서 각 row들의 최솟값을 구하고 각 row들의 loss를 전에 구한 최솟값으로 row 값들을 빼주는 row reduction 과정을 거칩니다. 위 식에서 i는 column의 갯수이고 j는 row의 갯수 입니다.

 

 

$$ 
l_{i,j} = l_{i,j} - min(l_j)
$$


이제 위와 같은 과정을 column에 대해서도 적용해줍니다. 이를 column reduction 이라 합니다.

 

이 과정을 거치고 난 후 마지막으로 0의 값을 갖는 것들에 대해 optimal인지에 대한 test를 진행하고 optimal한 unique matching을 가능하게 합니다. (막무가내로 다 확인했을 때보다 훨씬 빠름._ Table의 크기가 클수록)

 

이 떄 Matching Cost인 \(L_{match}(y_i,\hat y_{\sigma (i)})\)는





이 식과 같습니다.

loss function




위의 hungarian algorithm을 거쳐 matching 된 것을 기반으로 하는 Hungarian loss를 사용합니다.
이 때 \(c \neq \varnothing\) 이면, 즉 no object라면 log probability를 10으로 나눠줬습니다. 이는 class의 불균형을 막아주기 위한 작업이라 합니다. (선택인듯?)





위 식의 Box Loss는 이와 같습니다. 이는 box 자체를 직접적으로 예측 함을 알 수 있습니다.

DETR architecture

 


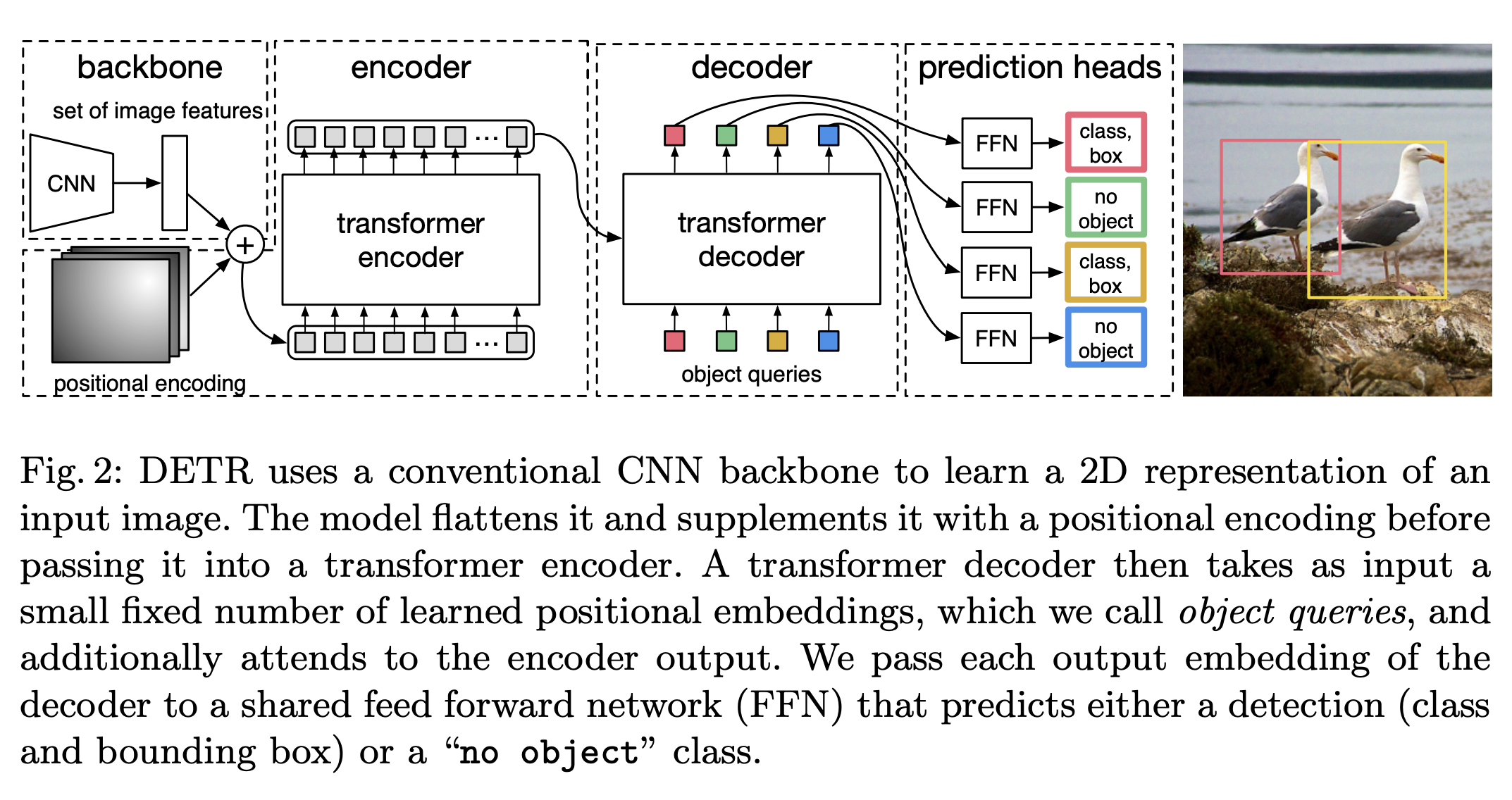
Fig.2.를 보시면 대략적인 형태를 알 수 있습니다. 각 backbone, encoder * N, decoder * M, prediction heads로 이뤄져 있습니다.

Backbone

[3xHxW]의 input을 받아서 backbone에 넘깁니다.





위 사진의 shape을 갖게 됩니다. (Resnet 50의 경우입니다.)
이건 정확한 지식은 아닌데 이 backbone을 통해 받은 feature가 local 즉 patch에 대한 정보를 가지고 있어서 이를 transformer에 넣었을 때 object detection에 의미 있는 정보가 나오는게 아닌지 생각이 들었습니다.

Positional Embedding

sin, cos를 사용한 Positional Encoding도 있지만, microsoft의 detr 코드를 보면 훈련 가능한 Positional embedding 형식으로 구성 되어 있습니다.


image는 row 방향 뿐만이 아닌 column 방향의 position information을 고려해줘야 합니다. 그래서 사용하는 embedding dimension을 2로 나눠서 column에 대한 positional 정보 (embed_dim/2)와 row에 대한 positional 정보 (embed_dim/2)를 concat 시켜 줍니다. 이렇게 되면 row, column 방향 모두를 고려한 positional embedding을 할 수 있습니다.

 

class PositionalEmbedding(nn.Module):
    def __init__(self, n_dim): # 실제 transformer에서 사용하는 embedding dimension
        super().__init__()
        self.embed_dim = int(n_dim/2)
        self.row_embed = nn.Embedding(50, self.embed_dim)
        self.col_embed = nn.Embedding(50, self.embed_dim)

    def reset_parameters(self):
        nn.init.uniform_(self.row_embed.weight)
        nn.init.uniform_(self.col_embed.weight)

    def forward(self, x):
        h,w = x.size()[-2:]
        i = torch.arange(w, device=x.device)
        j = torch.arange(h, device=x.device)
        x_embed = self.col_embed(i) # w, embed_dim
        y_embed = self.row_embed(j) # h, embed_dim

        pos = torch.cat([
                            x_embed.unsqueeze(0).repeat(h,1,1),
                            y_embed.unsqueeze(1).repeat(1,w,1)
                            ], dim=-1).permute(2,0,1).unsqueeze(0).repeat(x.shape[0],1,1,1)
        return pos


코드는 위와 같고, embedding을 통해 positional information을 학습시킵니다. 보통 찾아보면 학습 가능한 Positional Embedding은 MHSA에 직접 들어가게 되는데 그 방법의 일종이지 않을까 생각이 듭니다.

Transformer Encoder Decoder




Encoder Decoder의 형태는 위와 같습니다.


Encoder에서 MHSA 등을 거치면서 positional 정보가 들어간 feature에 대해 자기 자신 안에서의 상호작용 정보를 파악한다는 정도와 input으로 들어갈 때 dxHW의 형태로 변환된다는 것 외에는 특별한 점이 없습니다.

 

Decoder의 경우에는 object queries라 되어있는데 이는 dimension으로는 embedding dim을 갖으며 seq_len으로는 예측할 것의 갯수만큼을 갖게 됩니다.


Decoder의 MHSA에서 자기 자신의 연관성을 고려한 어떤 값을 갖게 되고 이를 두번쨰 sub layer의 MHA에 Query로서 들어가게 됩니다.


이 query는 Encoder에서 output, 즉 image features에서 상호작용 정보를 고려한 값들 (image features * scaled Dot Product Attention)을 key, value로서 받게 됩니다.


MHA에서는 image features에서 상호작용 정보 및 위치 정보가 고려된 key와 처음 임의로 초기화 됐고 자기 자신의 상호작용 정보가 고려된 Query의 상호작용 정보가 고려된 값을 내보내게 됩니다.


그래서 이 정보를 기반으로 Prediction을 하게 됩니다.

말이 복잡해서 간단히 정리해봤습니다.





Transformer에 대한 코드는 아래와 같습니다.

import copy
import torch
import torch.nn as nn


# num queries : 예측할 object 갯수.

class Transformer(nn.Module):
    def __init__(self, d_model=512, nhead=8, num_encoder_layers=6,
                 num_decoder_layers=6, dim_feedforward=2048, dropout=0.1, ):
        super().__init__()
        encoder_layer = TransformerEncoderLayer(d_model, nhead, dim_feedforward, dropout)

        self.encoder = TransformerEncoder(encoder_layer, num_encoder_layers)
        self.d_model = d_model

        decoder_layer = TransformerDecoderLayer(d_model, nhead, dim_feedforward, dropout)
        decoder_norm = nn.LayerNorm(d_model)
        self.decoder = TransformerDecoder(decoder_layer, num_decoder_layers, decoder_norm)

    def forward(self, src, query_embed, pos_embed):
        # flatten NxCxHxW to HWxNxC
        bs, c, h, w = src.shape
        src = src.flatten(2).permute(2, 0, 1)
        pos_embed = pos_embed.flatten(2).permute(2, 0, 1)
        query_embed = query_embed.unsqueeze(1).repeat(1, bs, 1)

        tgt = torch.zeros_like(query_embed)
        memory = self.encoder(src, pos=pos_embed)
        hs = self.decoder(tgt, memory, query_pos=query_embed)
        return hs.transpose(1, 2), memory.permute(1, 2, 0).view(bs, c, h, w)


class TransformerEncoder(nn.Module):
    def __init__(self, encoder_layer, layer_num, norm=None):
        super().__init__()
        self.layers = clone_layer(encoder_layer, layer_num)
        self.norm = norm

    def forward(self, src, pos=None):
        out = src
        for layer in self.layer:
            out = layer(out, pos)

        if self.norm:
            out = self.norm(out)

        return out


class TransformerDecoder(nn.Module):
    def __init__(self, decoder_layer, layer_num, norm=None):
        super().__init__()
        self.layers = clone_layer(decoder_layer, layer_num)
        self.norm = norm

    def forward(self, tgt, memory, pos=None, query_pos=None):
        out = tgt
        for layer in self.layers:
            out = layer(out, memory, pos, query_pos)
        if self.norm:
            out = self.norm(out)
        return out


class TransformerEncoderLayer(nn.Module):
    def __init__(self, d_model=512, n_head=8, dim_feedforward=2048, dropout=0.1):
        super().__init__()
        self.self_attn = nn.MultiheadAttention(d_model, n_head, dropout=dropout)
        self.linear1 = nn.Linear(d_model, dim_feedforward)
        self.activation = nn.ReLU()
        self.dropout = nn.Dropout(dropout)

        self.dropout1 = nn.Dropout(dropout)
        self.linear2 = nn.Linear(dim_feedforward, d_model)
        self.dropout2 = nn.Dropout(dropout)

        self.norm1 = nn.LayerNorm(d_model)
        self.norm2 = nn.LayerNorm(d_model)

    def forward(self, src, pos=None):
        q = k = self.pos_add(src, pos)
        src2 = self.self_attn(q, k, value=src)[0]
        src = src + self.dropout(src2)
        src = self.norm1(src)

        src2 = self.linear2(self.dropout1(self.activation(self.linear1(src))))
        src = src + self.dropout2(src2)
        src = self.norm2(src)

        return src

    def pos_add(self, src, pos):
        return src if pos == None else src + pos


class TransformerDecoderLayer(nn.Module):
    def __init__(self, d_model=512, n_head=8, dim_feedforward=2048, dropout=0.1):
        super().__init__()
        self.self_attn = nn.MultiheadAttention(d_model, n_head, dropout=dropout)
        self.mh_attn = nn.MultiheadAttention(d_model, n_head, dropout=dropout)

        self.linear1 = nn.Linear(d_model, dim_feedforward)
        self.activation = nn.ReLU()
        self.dropout = nn.Dropout(dropout)
        self.linear2 = nn.Linear(dim_feedforward, d_model)

        self.norm1 = nn.LayerNorm(d_model)
        self.norm2 = nn.LayerNorm(d_model)
        self.norm3 = nn.LayerNorm(d_model)

        self.dropout1 = nn.Dropout(dropout)
        self.dropout2 = nn.Dropout(dropout)
        self.dropout3 = nn.Dropout(dropout)

    def forward(self, tgt, memory, pos=None, query_pos=None):
        q = k = self.pos_add(tgt, query_pos)

        tgt2 = self.self_attn(q, k, value=tgt)[0]

        tgt = tgt + self.dropout1(tgt2)
        tgt = self.norm1(tgt)

        tgt2 = self.mh_attn(self.pos_add(tgt, query_pos), self.pos_add(memory, pos), value=memory)[0]
        tgt = tgt + self.dropout2(tgt)
        tgt = self.norm2(tgt)

        tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))

        tgt = tgt + self.dropout3(tgt2)

        return tgt

    def pos_add(self, tensor, pos):
        return tensor if pos == None else tensor + pos


def clone_layer(layer, layer_num):
    return [copy.deepcopy(layer) for _ in range(layer_num)]

Reference

DETR paper : https://arxiv.org/abs/2005.12872
Microsoft detr github : https://github.com/facebookresearch/detr
Hungarian Algorithm : https://www.youtube.com/watch?v=cQ5MsiGaDY8&t=0s

728x90

'Computer Vision' 카테고리의 다른 글

Vision Transformer의 이해와 Swin Transformer  (4) 2021.05.21
[논문 리뷰] Deformable DETR : Deformable Transformers For End-To-End Object Detection  (1) 2021.05.21
[논문 리뷰] FPN : Feature Pyramid Networks for Object Detection  (0) 2021.05.20
[논문 리뷰] Deep Networks with Stochastic Depth  (0) 2021.05.20
[논문 리뷰] EfficientNet : Rethinking Model Scaling for Convolutional Neural Networks  (0) 2021.05.20

'Computer Vision' Related Articles

티스토리툴바