https://github.com/yhy258/Stochastic_depth_resnet50
Abstract
지금까지 benchmarks에 대한 error를 놀랍게 낮췄던 CNN의 진보는 Very Deep Convolutional Networks입니다. 하지만 이렇게 깊은 depth를 갖은 convolutional networks의 경우, train 시 어려움이 있습니다. (Vanishing Gradients, train time ...)
이에 대한 해결책으로 논문에서는 Stochastic depth를 제안합니다. train 시 short network를 사용하고 test 시 deep network를 사용합니다.
이 stochastic depth는 layer의 부분을 무작위로 drop하는 방법입니다. 그리고 identity function으로 bypass를 진행합니다. 이를 통해서 train 시간을 줄였고 test 시 error도 줄였습니다.
Introduction
Network의 depth는 model expressiveness에서의 주요 결정 요인입니다. 하지만 very deep network는 vanishing gradient, diminishing feature 등의 현상을 일으킵니다.
Diminishing feature : Forward 시 여러번 multiplication, convolution computation 을 반복하면서 Feature가 손실되는 현상
Very deep convolutional network 연구에서의 inherent dilemma가 존재하는데 이는 shorter network의 경우 효율적인 training이 가능하지만, 복잡한 concept에 대해 expressive 하지 않다는 점이고, 반면에 Very deep networks의 경우에는 훨씬 더 큰 model complexity를 갖을 수 있지만 훈련이 어렵다는 점 입니다.
이 dilemma에 대해서 stochastic depth를 제안합니다. 모순되긴 하지만 training 시에는 short network, test시에는 deep network를 사용합니다.
이 stochastic depth를 통해서 test error를 줄였는데, 이에 대한 요인은 두가지로 볼 수 있습니다.
- depth를 줄여서 training 중의 forward propagation 및 gradient computation의 chain을 감소시킴.
- stochastic depth의 경우, implicit ensemble로 볼 수 있음. (network에 대해 다른 depth를 사용)
Deep Networks with Stochastic Depth

Stochastic Depth에 대해 Fig. 2.가 잘 설명 해주고 있습니다.
우선 skip하는 기준은 \(b_l \in {0,1}\) 인 베르누이 랜덤 변수에 의해 정해집니다. 여기에서 만약 \(l\)번쨰 레이어의 베르누이 랜덤 변수가 1이라면 active하고 아니라면 inactive 하게 됩니다. 여기에서 layer \(l\) 이 "survival" 하는 probability를 \(p_l = Pr(b_l=1)\)로 표현 했습니다.

그래서 \(l\)번째 레이어가 active 했을 때의 식은 위와 같습니다.

위의 식은 \(b_l = 0\) 일 때 입니다.
근데 이 stochastic depth에서는 식의 \(H_{l-1}\)은 무조건 non-negative하다고 가정 했습니다. 물론 activation function이 relu이기 때문에 성립하긴 하지만 첫 레이어일 경우를 고려해야 하기 때문에 \(l\geq 2\)여야 합니다.
The survival probabilities
앞에서 survival probabilites를 언급 했는데 이 때 \(p_l\)은 하이퍼파라미터 인데, 이 값은 이웃한 blocks와 비슷한 값을 가져야 합니다. 가장 간단한 방법으로는 일률적으로 전부 정하는 방법이 있습니다.
다른 방법은 \(l\)에 대한 smooth function을 통해 정하는 것 입니다.

smooth function은 위와 같습니다. 여기에서 요지는 \(p_0=1\)에 대해서 linearly decay를 시행합니다. \(L\)은 마지막 레이어를 뜻합니다. 그리고 이 마지막 레이어에 대한 survival probability를 \(p_L = 0.5\)로 설정 합니다.
Expected network depth
transformation \(f_l\)에 대해 \((1-p_l)\)의 확률로 bypass하게 됩니다.
stochastic depth에 대해 training 시의 effective ResBlock의 수는 \(E(\tilde L) = \sum^L_{l=1}p_l\)이 됩니다. 이 때 L이 크면, \(E(\tilde L) \approx 3L/4\)에 수렴하게 됩니다.
Stochastic depth during testing
test 시에는 survival probability에 대해 고려해줘야 합니다. 그래서 식은 아래와 같이 나옵니다.
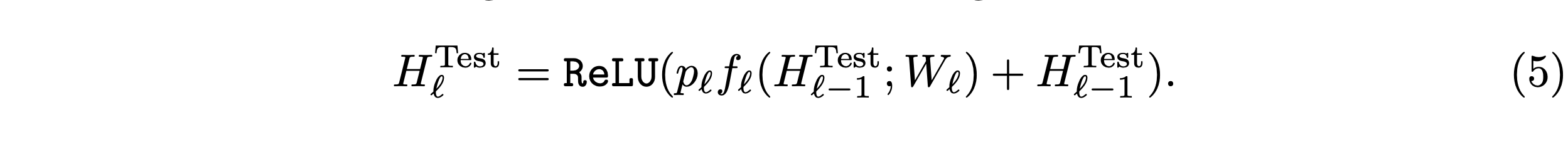
Improved gradient strength
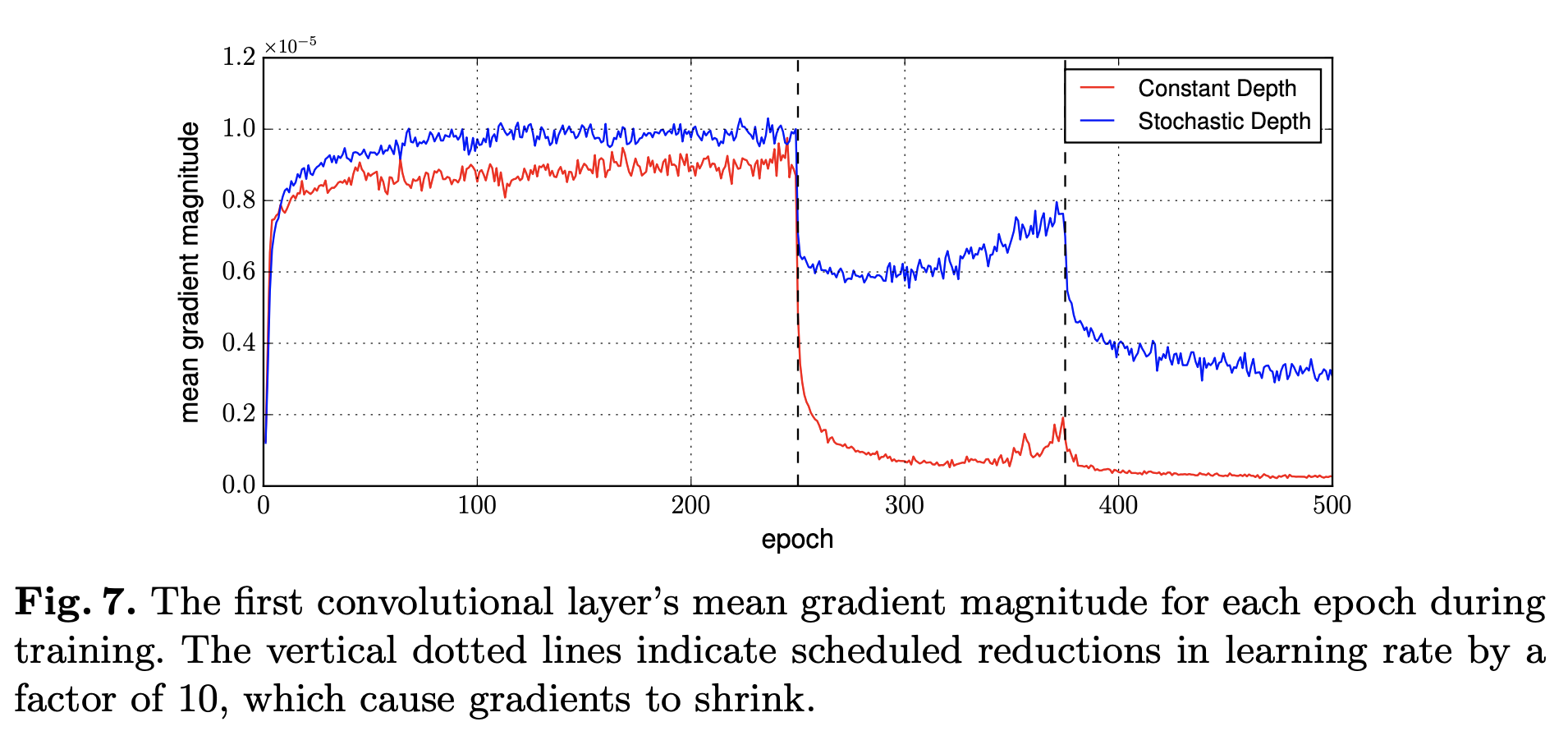
Fig.7과 같이 Stochastic depth 적용 시 Graident Descent가 많은 정보를 담음을 알 수 있습니다. 이는 효과적인 model의 훈련을 돕습니다.

