GAN을 공부하면서 Minimax Game의 Nash Equilibrium에 대해 알아가고 있는 차에 Non Convex, Non Concave 상황에서의 문제는 제대로 작동하지 않을 것 같아 새로운 논문을 보다가 찾게 되었습니다.
Nash Equilibrium 에 대해 "아 그냥 그렇구나" 하고 넘어갔던 부분을 세세히 집고 해당 문제점을 포괄할 수 있는 새로운 정의를 내린 논문입니다.
https://arxiv.org/pdf/1902.00618.pdf
Abstract
기존의 Minimax Game에 대한 연구들은 Simultaneous Game에 집중하고 있습니다. Simultaneous Game이란 Minimax Game player A, B가 동시에 행동함을 말합니다.
하지만 실제로 최적화 문제의 minimax game은 Sequential Game인 경우가 많습니다. (First, Second Player가 나눠진.) 그래서 Simultaneous Game에서의 이론은 적용되기 힘듭니다.
Sequential Game은 당연히 아래 식을 만족합니다.
$$ \min_x\max_y f(x, y) \neq \max_y\min_x f(x, y) $$
그리고 기존의 Nash Equilibrium에 대해서 Nonconcave, Nonconvex function인 경우에는 해당 정의를 만족하지 않을 수 있습니다.
위의 이유들로 새로운 Minimax Optimization에 대한 정의가 필요함을 알 수 있습니다.
Introduction
What is a good notion of local optimality in nonconvex-nonconcave minimax optimization?
어떤 표현이 nonconvex-nonconcave minimax optimization에서 최적이라 할 수 있을까요?
본 논문에서는 optimal solution \( (x^*, y^*) \)을 two player sequentiual game에서 정의하며 시작합니다.
\( \min_x\max_y f(x,y) \)에서 \(y^*\)는 \(f(x^*, .)\)의 global maximum이고 이 때 \(x^*\)는 \(\phi(x):=\max_{y\in Y}f(x,y)\)에서의 global minimum 입니다.
이 논문에서의 주목해야 할 점은 local minimax 입니다. Local Nash Equilibrium을 포괄하는 좀 더 넓은 정의라고 생각하시면 좋을 것 같습니다.
Simultaneous games (이전 연구)
Definition : Nash Equilibrium
Point \(x^*, y^*\)가 Nash equilibrium이면, 어떤 x, y에서도 아래 식을 만족합니다.
$$ f(x^*,y) \leq f(x^*,y^*) \leq f(x, y^*) $$
Definition : Local Nash Equilibrium
Point \(x^*, y^*\)가 Local Nash Equilibrium이면, \(||x-x^*||\) and \(||y-y^*||\)에서
$$ f(x^*,y) \leq f(x^*,y^*) \leq f(x, y^*) $$
을 만족하는 어떤 \(\delta > 0\)이 존재합니다.
First Order Necessary Condition
f가 미분 가능하다고 가정. \(\nabla_xf(x,y)=0\), \(\nabla_yf(x,y)=0\) 를 만족합니다.
Second Order Necessary Condition
f가 두번 미분 가능다고 가정. \(\nabla^2_{xx}f(x,y)\geq 0\), \(\nabla^2_{yy}f(x,y)\leq 0\)
Second Order Sufficient Condition
f가 두번 미분 가능다고 가정. \(\nabla^2_{xx}f(x,y) > 0\), \(\nabla^2_{yy}f(x,y) < 0\)
이는 strict local nash equilibrium이라 합니다.
근데 여기에서 중요한 점은 두 번 미분 가능하지만 nonconvex-nonconcave인 경우에 위 성질이 들어맞지 않는 경우가 생깁니다.
예를 들어 \(f(x,y) = sin(x + y)\)라고 하면, 위의 First Order Necessary Condition을 만족하면서 Second Order Necessary Condition을 만족하는 지점은 없음을 알 수 있습니다.
(Simultaneous Game이라 할지라도 nonconvex-nonconcave라면 예외의 경우가 발생한다.)
Sequential Game
Sequential Game의 중요한 점은 두번째 player가 첫번째 player의 행동을 관찰하고 이에 따라 움직일 수 있다는 점 입니다.
본 논문에서는 \(\min_x\)를 먼저 진행하고 \(\max_y\)를 진행한다고 가정합니다. 즉 식을 아래와 같이 표현할 수 있습니다.
$$ \min_{x\in X}\max_{y\in Y}f(x,y) $$
$$ \min_{x\in X}\max_{y\in Y}f(x,y) \neq \max_{y\in Y}\min_{x\in X}f(x,y) $$
이 상황에서 global solution은 Stackelberg equilibrium 이라고 할 수 있습니다.
Stackelberg Equilibrium
두번째 player는 x의 어떤 action이 주어지던, 언제나 f(x, .)의 maximize이고 \(\phi(x) := \max_{y'\in Y}f(x,y)\)에서의 maximum value \(\phi(x)\)를 얻습니다.
그리고 첫번째 player의 optimal strategy는 \(\phi(x)\)를 minimize하는 것 입니다. 이 때 global optimality의 Definition을 따라야합니다.
Definition : Global minimax point
global minimax point \(x^*, y^*\)는 어떤 (x,y) 에 대해 아래 식을 만족합니다.
$$ f(x^*,y) \leq f(x^*,y^*) \leq \max_{y'\in Y}f(x,y') $$
차례를 고려해줬다고 생각하면 됩니다. minimize -> maximize이기 때문에 우항이 이와 같이 표현되었음을 알 수 있습니다.
그리고 Nash Equilibria와 다르게 최대 최소 정리에 의거하여 global minimax point가 언제나 존재한다고 합니다. 단 x, y가 상주하는 X, Y 공간이 compact하다는 가정하에 만족한다고 합니다. (이 부분은 잘 모르겠네요..)
Dynamical Systems
본 논문에서는 최적화 방법을 점근적인 Gradient Descent Ascent (GDA)로 제한했습니다.
Definition : Fixed Point
\(z^*\) : \(z^*=w(z^*)\)
여기에서 w는 update system을 의미합니다. (gradient를 더하거나 빼서 update 하는 행위를 function으로 나타냄)
Main Results
본 논문에서는 local minimax 라는 definition을 새로 정의 합니다.
Definition : Local minimax point
\((x^*, y^*)\).
\(\delta_0 >0\)과 \(\delta \in (0,\delta_0]\), \(\delta \rightarrow 0\) 함에 따라 \(h(\delta)\rightarrow 0\)인 function h 가 존재하고 어떤 \(x,y\)가 \(||x-x^*|| \leq \delta\), \(||y-y^*|| \leq \delta\)를 만족할 때 아래 식을 만족하면 \((x^*, y^*)\).을 Local Minimax Point 라고 합니다. (h는 단조함수 느낌 ?)
$$ f(x^*, y)\leq f(x^*, y^*) \leq \max_{y' : ||y'-y^*||\leq h(\delta)}f(x,y') $$
위의 조건에서 중요하게 볼 부분이 두가지 정도 존재합니다.
- 약간의 전략 변화를 허가했음. \(y'\)는 \(y^*\)의 주변임.
- x, y Sequential 한 게임이라서 차례에 따라 변동성이 다를 수 있음. \(h(\delta)\) 를 통해 고려해줌.
이 부분이 Local Nash Equilibrium과의 중요한 차이점이라 볼 수 있습니다.
그리고 Local minimax point는 아래 조건을 만족합니다.
First Order Necessary Condition
f가 미분 가능하다고 가정. \(\nabla_xf(x,y)=0\), \(\nabla_yf(x,y)=0\) 를 만족합니다.
Second Order Necessary Condition
f가 두번 미분가능하다고 가정. \(\nabla^2_{yy}f(x,y)\leq 0\)이고, \(\nabla^2_{yy}f(x,y) < 0\)까지 만족하면, Hessian의 Schur Complement가 0 이상임을 보장합니다. 아래 식이 이를 의미합니다.

이에 대한 증명은 논문의 Appendix 에 잘 나와있습니다. 위 식은 \(f(x^*,y^*)\)의 주변을 고려하여 (local minimax 임을 활용함.) 전개해나갑니다.
Second Order Sufficient Condition
f가 두번 미분가능하다고 가정. 어느 stationary point \((x, y)\)도 \(\nabla^2_{yy}f(x,y) < 0\)를 만족하게 됩니다. 그리고 Schur Complement를 strict하게 만족합니다.
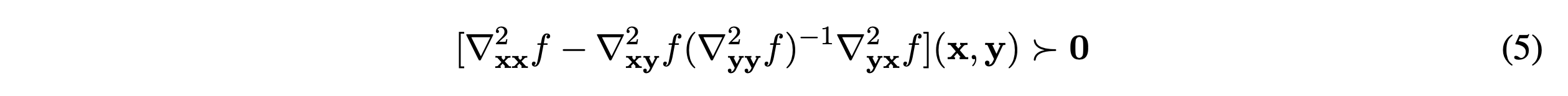
이러한 stationary point를 strict local minimax point라고 명명합니다.

논문의 Figure 1 입니다. Local Nash 이면서 local minimax 일 수 있지만, Local minimax이면서 local nash가 아닌 경우를 보여줍니다.
Local Nash보다 Local Minimax가 좀 더 큰 범위라고 생각할 수 있습니다. 위의 figure의 우측을 보면 x, y축으로 뒤틀려 있는데 이런 경우에 x,y의 사이 관계에 대해 고려를 할 수 있어야 합니다.
Local Nash의 필요 조건들은 이를 전혀 고려하지 않기 때문에 우측 사진에서는 local nash일 수 없음을 알 수 있습니다. 반면, Local minimax의 경우 Schur Complement 형식으로, Hessian의 xy, yx block을 고려해주기 때문에 축이 다소 뒤틀려 있어도 문제 없이 평형점을 포착할 수 있습니다.
second player가 first player의 action에 따라 취하는 action이 달라질 수 있다는 사실을 통해 직관적으로도 위와 같음을 알 수 있습니다.
본 논문을 더 읽다보면 \(\gamma-GDA\), \(\infty-GDA\)를 통해 Local Nash와 Local minimax 사이 관계를 좀 더 풀어나가는 부분이 나오는데 직접 읽어보시는걸 추천드립니다.
'Others' 카테고리의 다른 글
| 최적화 공부 (0) | 2022.02.11 |
|---|---|
| [논문 리뷰] SAM Optimizer : Sharpness-Aware Minimization for Efficiently Improving Generalization (0) | 2021.05.20 |
| [논문 리뷰] : Manifold Mixup : Better Representations by Interpolating Hidden States (0) | 2021.05.20 |
| [논문 리뷰] mixup : Beyond Empirical Risk Minimization (0) | 2021.05.20 |
| Deep Neural Network 경량화 (Inception, Xception) (0) | 2021.05.19 |

