Epsilon Greedy
현재 상황(Optiaml하지 않음)에서 내가 가지고 있는 정보를 기반으로 최적의 선택으로 하려고 합니다. 하지만 동시에 이게 진짜 최적의 선택인가에 대한 의문 또한 품어야합니다.
그럼 내가 가지고 있는 정보 기반으로 최적의 선택만 해야할까요??
아닙니다. 만약 그렇게 된다면 더 나은 길을 못 볼 수도 있습니다. 그렇기 때문에 어느정도 삐딱선을 타야합니다.
최적의 선택을 함에 있어서 삐딱선을 탐은 Exploration을 의미합니다. 현재 정보에 의존하지 않고 그냥 랜덤으로 action을 정하는 거예요.
그리고 단순히 내가 가지고 있는 정보를 기반으로 최적의 선택을 하는 것을 Exploitation이라고 하고, 그저 Exploitation을 수행하는 것을 Greedy 라고 합니다.
위처럼 단순히 Greedy만 수행한다면 더 나은 길을 못찾을 거예요. 그래서 어느정도의 Exploration도 동반하기 위해서 Epsilon Greedy라는 방법을 사용합니다. 이는 hyperparameter epsilon 값의 확률만큼 exploration을 진행함을 의미합니다. (그 확률 만큼 그냥 random으로 action을 취하는 거죠.)
rand = random.random()
if rand > self.eps:
values = self.get_values()
max_value = max(values)
indices = [i for i, value in enumerate(values) if value == max_value]
max_value_idx=random.choice(indices)
act = max_value_idx + 1
else :
act = random.choice(self.action_name)코드로서는 위 과정에 해당합니다.
행동 가치 방법
그럼 위에서 말하는 내가 가진 정보는 뭘 의미하는 걸까요?? 이는 행동의 가치에 해당합니다.
나중에 더 나은 방법이 나오겠지만 현재는 간단하게 표본평균을 사용합니다.
이는 해당 Action으로부터 나온 Reward들을 해당 Action을 취한 횟수로 나눈 것입니다. 그 말대로 해당 Action에 대한 평균입니다.
K-armed testbed : 임의로 설정한 Environment
K-armed testbed는 K개의 레버를 만들어 놓고 임의로 각 레버의 보상에 대한 분포를 정하여 Environment를 임의로 만드는 것을 의미합니다.
Stationary, Unstationary
Stationary : 각 레버의 분포가 고정.
Unstationary : 각 레버의 분포가 고정되지 않고 계속 변함.
점증적 구현
우리는 임의로 실행해가며 여러번 레버를 당겨 볼 겁니다. 근데 당겨보는 횟수가 많아지면 표본 평균을 구하는데 상당한 계산 필요할 수도 있습니다. 이보다는 수치 계산 측면에서 효율적으로 계산하는 방법이 필요할 것 같습니다.
평균을 구하는 과정을 넣는게 아닌 점증적으로 평균을 내놓는 방법을 강구할 수 있습니다.
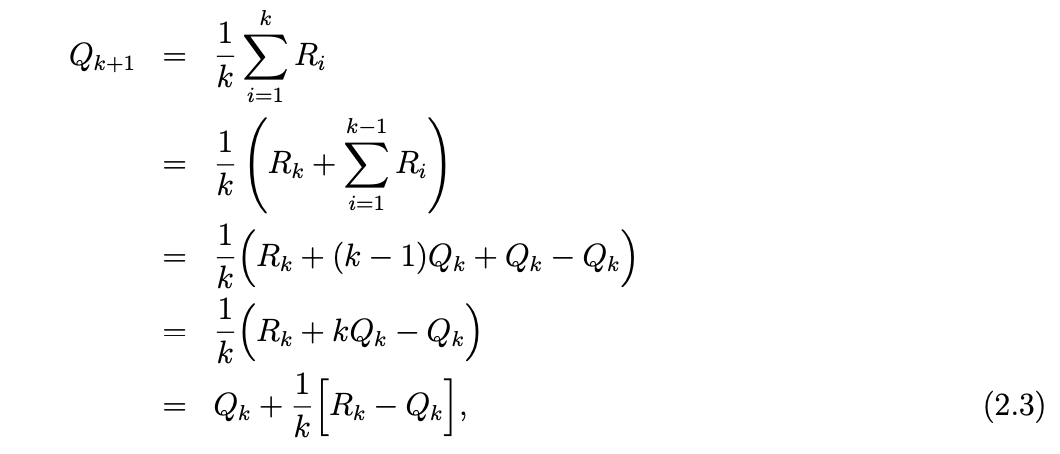
k+1 시점에서의 표본 평균을 위와 같이 점증적인 형식의 식으로 나타낼 수 있습니다.
Unstationary Problem
문제들 중에서는 Stationary한 문제들보다 Unstationary한 문제들이 더 많습니다.
위의 점증적인 식을 한번 봐봅시다. discount step으로 볼 수 있는 1/k는 아래 식을 만족하기 때문에 수렴성을 보장받을 수 있었습니다.
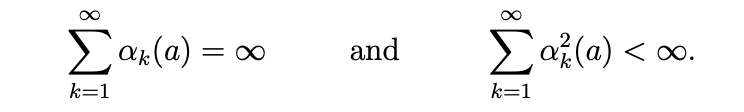
하지만 time step이 아닌 fixed value를 사용한다면 두번째 조건을 만족하지 못합니다. 이는 수렴하지 못한다 라고 생각될 수 있습니다. 이는 최근에 받은 보상일 수록 그에 더 반응하여 연속적으로 변함을 의미합니다.(수렴하지 않으니까)
그러므로 Unstationary Problem에는 fixed value를 사용하는게 더 바람직합니다.
Unstationary Problem에서 fixed value 와 time step 사용의 차이에 대한 결과

구현 Github : https://github.com/yhy258/ReinforceLearning-Study/tree/main/Sutton/10Armed
'Reinforcement Learning' 카테고리의 다른 글
| [Just Code] 다중 선택 (0) | 2021.05.21 |
|---|